Difficulty Level – 5: Very Difficult
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $n$ is a number greater than −1 but smaller than 0, which of the following properly lists numbers from smallest to largest?
$n^3 \lt n^2 \lt n$ | |
$n \lt n^2 \lt n^5$ | |
$n \lt 2n \lt − 3n$ | |
$2n \lt n^3 \lt \dfrac{n}{− 2}$ | |
$n \lt n^2 \lt n^3$ |
Question 1 Explanation:
The correct answer is (D). The easiest way to solve problems involving particular conditions and an unknown variable is to choose our own number that satisfies the conditions and then test the answer choices. Here we must choose a number that is −1 < $n$ < 0, so $n = −\frac{1}{2}$ would make a good choice.
Right away we can see that because our value is negative, every even power we raise it to must be larger (since it will be positive) than any odd power we raise it to (since it will be negative), thus we can eliminate answer choices (A) (B) and (E).
Testing choice (C):
$-\dfrac{1}{2} \lt 2 * -\dfrac{1}{2} \lt -3 * -\dfrac{1}{2}$
$ \to -\dfrac{1}{2} \lt -1 \lt \dfrac{3}{2}$
This fails because −1 is not greater than $-\frac{1}{2}$, thus answer choice (D) must be correct.
$2n < n^3 < \frac{n}{-2}$
$2 \ast -\frac{1}{2} < \left(-\frac{1}{2}\right)^3 < \dfrac{\left(-\frac{1}{2}\right)}{-2}$
$-1 < -\frac{1}{8} < \frac{1}{4}$
Right away we can see that because our value is negative, every even power we raise it to must be larger (since it will be positive) than any odd power we raise it to (since it will be negative), thus we can eliminate answer choices (A) (B) and (E).
Testing choice (C):
$-\dfrac{1}{2} \lt 2 * -\dfrac{1}{2} \lt -3 * -\dfrac{1}{2}$
$ \to -\dfrac{1}{2} \lt -1 \lt \dfrac{3}{2}$
This fails because −1 is not greater than $-\frac{1}{2}$, thus answer choice (D) must be correct.
$2n < n^3 < \frac{n}{-2}$
$2 \ast -\frac{1}{2} < \left(-\frac{1}{2}\right)^3 < \dfrac{\left(-\frac{1}{2}\right)}{-2}$
$-1 < -\frac{1}{8} < \frac{1}{4}$
Question 2 |
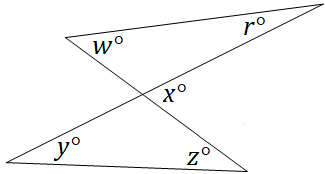
In terms of $x$, what is the sum of the angles $r$, $w$, $y$, and $z$?
$360 − x$ | |
$180 − x$ | |
$2x$ | |
$\dfrac{3}{2}x$ | |
$4x$ |
Question 2 Explanation:
The correct answer is (C). We will need to rely upon knowledge of straight lines and triangle interior angle sums to answer this question.
According to the "exterior angle theorem", in any triangle, the sum of two interior opposite (remote) angles is equal to the value of the corresponding exterior angle.
$w + r = x$
$y + z = x$
$w + r + y + z = x + x $ $ = 2x$
According to the "exterior angle theorem", in any triangle, the sum of two interior opposite (remote) angles is equal to the value of the corresponding exterior angle.
$w + r = x$
$y + z = x$
$w + r + y + z = x + x $ $ = 2x$
Question 3 |
For the triangle below, $\sin(z) = \dfrac{7}{25}$. What is the value of $y$?
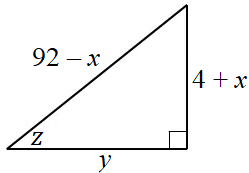
$72$ | |
$24$ | |
$27$ | |
$84$ | |
$65$ |
Question 3 Explanation:
The correct answer is (A). We are given $\sin(z) = \frac{7}{25}$, which is the ratio of the opposite side to the hypotenuse.
$\dfrac{7}{25} = \dfrac{4 + x}{92 - x}$
Solving for $x$:
$(7)(92 - x) = (25)(4 + x)$
$644 - 7x = 100 + 25x$
$544 = 32x$
$x = 17$
Use $x = 17$ to find the lengths of two sides of the triangle:
Opposite $= 4 + x = 4 + 17 = 21$
Hypotenuse $= 92 - x = 92 - 17 = 75$
We can solve for $y$, the adjacent side, using the Pythagorean Theorem:
$21^2 + y^2 = 75^2$
$441 + y^2 = 5625$
$y^2 = 5184$
$y = 72$
$\dfrac{7}{25} = \dfrac{4 + x}{92 - x}$
Solving for $x$:
$(7)(92 - x) = (25)(4 + x)$
$644 - 7x = 100 + 25x$
$544 = 32x$
$x = 17$
Use $x = 17$ to find the lengths of two sides of the triangle:
Opposite $= 4 + x = 4 + 17 = 21$
Hypotenuse $= 92 - x = 92 - 17 = 75$
We can solve for $y$, the adjacent side, using the Pythagorean Theorem:
$21^2 + y^2 = 75^2$
$441 + y^2 = 5625$
$y^2 = 5184$
$y = 72$
Question 4 |
What is the average of the solution set of the inequality $|−2x + 4| \lt 6?$
$−3$ | |
$−2$ | |
$0$ | |
$2$ | |
$3$ |
Question 4 Explanation:
The correct answer is (D). In order to find the average of the set of solutions, we must first solve the inequality:
$|-2x + 4| < 6$
When solving inequalities involving absolute value, begin by rewriting as two separate inequalities:
i) $(-2x + 4) < 6$
and
ii) $-(-2x + 4) < 6$
Solving each, we get:
i) $-2x + 4 < 6$
$-2x < 2$
$x > -1$
(Note: When dividing by a negative number, we must flip the inequality symbol)
ii) $-(-2x + 4) < 6$
$2x - 4 < 6$
$2x < 10$
$x < 5$
Now that we have the solution set, we can find its average by summing the extreme values and dividing by 2:
$\dfrac{5+(-1)}{2}=\dfrac{4}{2}=2$
$|-2x + 4| < 6$
When solving inequalities involving absolute value, begin by rewriting as two separate inequalities:
i) $(-2x + 4) < 6$
and
ii) $-(-2x + 4) < 6$
Solving each, we get:
i) $-2x + 4 < 6$
$-2x < 2$
$x > -1$
(Note: When dividing by a negative number, we must flip the inequality symbol)
ii) $-(-2x + 4) < 6$
$2x - 4 < 6$
$2x < 10$
$x < 5$
Now that we have the solution set, we can find its average by summing the extreme values and dividing by 2:
$\dfrac{5+(-1)}{2}=\dfrac{4}{2}=2$
Question 5 |
What is the y-intercept of:
$g^{-1} (x)+2$ if $g(x)=\dfrac{-3x-7}{4}$$−\dfrac{2}{3}$ | |
$−\dfrac{1}{3}$ | |
$−\dfrac{7}{3}$ | |
$\dfrac{2}{3}$ | |
$\dfrac{1}{3}$ |
Question 5 Explanation:
The correct answer is (B). This question requires knowledge of inverses of functions to solve. Recall that to find the inverse of a function, we switch the input variable with the output variable and solve the new equation for the output variable. For example:
$y=\dfrac{-3x-7}{4}$
$ \to x= \dfrac{-3y-7}{4}$
Solving for $y$:
$4x=-3y-7$
$ \to -3y=4x+7$
$ \to y=-\dfrac{4}{3}x-\dfrac{7}{3}$
We have solved for the inverse of the function, but we must now locate the y-intercept when this entire function is moved vertically 2 spaces, as indicated by $g^{-1} (x) + 2$. We can make this translation by adding 2 to the equation:
$y=-\dfrac{4}{3}x-\dfrac{7}{3}+\dfrac{6}{3}$
$y=-\dfrac{4}{3}x-\dfrac{1}{3}$
We set $x = 0$ to solve for the y-intercept:
$y=-\dfrac{1}{3}$
$y=\dfrac{-3x-7}{4}$
$ \to x= \dfrac{-3y-7}{4}$
Solving for $y$:
$4x=-3y-7$
$ \to -3y=4x+7$
$ \to y=-\dfrac{4}{3}x-\dfrac{7}{3}$
We have solved for the inverse of the function, but we must now locate the y-intercept when this entire function is moved vertically 2 spaces, as indicated by $g^{-1} (x) + 2$. We can make this translation by adding 2 to the equation:
$y=-\dfrac{4}{3}x-\dfrac{7}{3}+\dfrac{6}{3}$
$y=-\dfrac{4}{3}x-\dfrac{1}{3}$
We set $x = 0$ to solve for the y-intercept:
$y=-\dfrac{1}{3}$
Question 6 |
The diameter of a sphere measures 5 inches. If a cube is inscribed inside the sphere, sharing its diagonal with the sphere’s diameter, what is the side length of the cube?
$3\sqrt{5}$ $\text{in.}$ | |
$5\sqrt{3}$ $\text{in.}$ | |
$\dfrac{5\sqrt{3}}{3}$ $\text{in.}$ | |
$5\sqrt{6}$ $\text{in.}$ | |
$6\sqrt{5}$ $\text{in.}$ |
Question 6 Explanation:
The correct answer is (C). As this question requires a couple spatial relationships, it may prove useful to draw a picture representing the situation. We are given that the diameter, which is the same as the diagonal of a cube, is equal to 5 inches. We also know that the diagonal of a cube is the hypotenuse of the right triangle constructed from one of the cube’s side lengths as well as the diagonal of one of the square faces of the cube.
Using this information we will set up an equation for the known relationships (Pythagorean’s Theorem) before solving for the target variable $s$, which represents the cube’s side length. We know that the hypotenuse of a cube’s square face is $s\sqrt{2}$ (recall that 45°, 45°, 90° right triangles have a side length relationship of $x,x, x \sqrt{2}$). We also know that one side length of the cube is $s$. Consequently:
$5^2=(s\sqrt{2})^2+s^2$
$ \to 25= 2s^2+s^2$
$ \to 25=3s^2$
$ \to \dfrac{25}{3}=s^2$
$ \to s = \dfrac{5}{\sqrt{3}}$
However, this answer choice is not found, so we must rationalize (remove the radical from) the denominator:
$\dfrac{5}{\sqrt{3}}*\dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{5 \sqrt{3}}{3}$ in.
Using this information we will set up an equation for the known relationships (Pythagorean’s Theorem) before solving for the target variable $s$, which represents the cube’s side length. We know that the hypotenuse of a cube’s square face is $s\sqrt{2}$ (recall that 45°, 45°, 90° right triangles have a side length relationship of $x,x, x \sqrt{2}$). We also know that one side length of the cube is $s$. Consequently:
$5^2=(s\sqrt{2})^2+s^2$
$ \to 25= 2s^2+s^2$
$ \to 25=3s^2$
$ \to \dfrac{25}{3}=s^2$
$ \to s = \dfrac{5}{\sqrt{3}}$
However, this answer choice is not found, so we must rationalize (remove the radical from) the denominator:
$\dfrac{5}{\sqrt{3}}*\dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{5 \sqrt{3}}{3}$ in.
Question 7 |
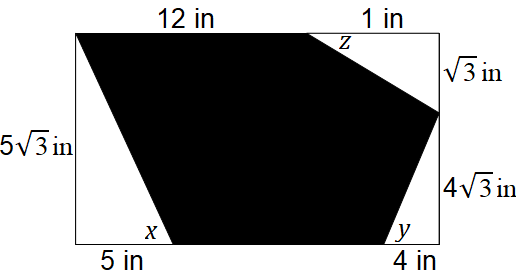
The figure above is composed of three right triangles drawn inside of a rectangle. What is the product of $\sin x$, $\cos y$, and $\tan z?$
$− 1$ | |
$1$ | |
$\dfrac{\sqrt{3}}{4}$ | |
$\dfrac{4}{\sqrt{3}}$ | |
$\dfrac{3}{4}$ |
Question 7 Explanation:
The correct answer is (E). Recall the acronym SOHCAHTOA, which stands for:
$ \sinθ = \dfrac{opp}{hyp}, \, $ $ \cosθ = \dfrac{adj}{hyp}, \, $ $ \tanθ = \dfrac{opp}{adj}$
Where $opp$ refers to the side opposite the angle, $adj$ refers to the side adjacent to the angle, and $hyp$ refers to the hypotenuse of the right triangle. Using these relationships, we will solve for $\sin x$, $\cos y$, and $\tan z$, then find their product.
$ \sin x =\dfrac{5\sqrt{3}}{10}, \, $ $ \cos y=\dfrac{4}{8}, \, $ $ \tan z= \dfrac{\sqrt{3}}{1}$
Recall that the hypotenuses for each of the triangles can be found using the Pythagorean Theorem, or by recalling the relationships of side lengths of 30°,60°,90° triangles. Now, combining to find the product:
$\dfrac{\sqrt{3}}{2}*\dfrac{1}{2}*\sqrt{3}=\dfrac{3}{4}$
$ \sinθ = \dfrac{opp}{hyp}, \, $ $ \cosθ = \dfrac{adj}{hyp}, \, $ $ \tanθ = \dfrac{opp}{adj}$
Where $opp$ refers to the side opposite the angle, $adj$ refers to the side adjacent to the angle, and $hyp$ refers to the hypotenuse of the right triangle. Using these relationships, we will solve for $\sin x$, $\cos y$, and $\tan z$, then find their product.
$ \sin x =\dfrac{5\sqrt{3}}{10}, \, $ $ \cos y=\dfrac{4}{8}, \, $ $ \tan z= \dfrac{\sqrt{3}}{1}$
Recall that the hypotenuses for each of the triangles can be found using the Pythagorean Theorem, or by recalling the relationships of side lengths of 30°,60°,90° triangles. Now, combining to find the product:
$\dfrac{\sqrt{3}}{2}*\dfrac{1}{2}*\sqrt{3}=\dfrac{3}{4}$
Question 8 |
What is one possible solution to the following equation:
$\dfrac{x+1}{x}-\dfrac{3}{2x^2}=-\dfrac{5}{2x}$
$− 1$ | |
$0$ | |
$\dfrac{−7+\sqrt{73}}{4}$ | |
$\dfrac{−7−\sqrt{25}}{4}$ | |
$−\dfrac{1}{2}$ |
Question 8 Explanation:
The correct answer is (C). This question may initially appear complicated, but by using the rules of combining fractions, we can greatly simplify the equation. In order to combine any fractions, we are required to find a common denominator. In this case, it can be seen that $2x^2$ is the best denominator to choose because the other fractions contain factors of it. Multiplying the necessary fractions we find:
$\dfrac{2x(x+1)}{2x(x)}-\dfrac{3}{2x^2} $ $ =\dfrac{x(-5)}{x(2x)}$
$\to \dfrac{2x^2+2x-3}{2x^2}=\dfrac{-5x}{2x^2}$
$\to 2x^2+2x-3=-5x$
$ \to 2x^2+7x-3=0$.
We can now use the quadratic formula to find what values of $x$ satisfy this equation. Recall that the quadratic formula is:
$x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
$ \to x= $ $ \dfrac{-7 \pm \sqrt{7^2-4(2)(-3)}}{2*2}$
$=\dfrac{-7 \pm \sqrt{73}}{4}$
$\dfrac{2x(x+1)}{2x(x)}-\dfrac{3}{2x^2} $ $ =\dfrac{x(-5)}{x(2x)}$
$\to \dfrac{2x^2+2x-3}{2x^2}=\dfrac{-5x}{2x^2}$
$\to 2x^2+2x-3=-5x$
$ \to 2x^2+7x-3=0$.
We can now use the quadratic formula to find what values of $x$ satisfy this equation. Recall that the quadratic formula is:
$x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
$ \to x= $ $ \dfrac{-7 \pm \sqrt{7^2-4(2)(-3)}}{2*2}$
$=\dfrac{-7 \pm \sqrt{73}}{4}$
Question 9 |
Which of the following is equivalent to:
$\dfrac{a}{3+b}-\dfrac{3}{b}+\dfrac{4-b}{a}$$\dfrac{ab^2 - 9a−3ab+12b−b^2−b^3}{ab(3+b)}$ | |
$\dfrac{ab^3 - 9b−3ab+12b−b^2−b^3}{ab(3+b)}$ | |
$\dfrac{ab^2+9a−3a^2b+12b−b^2−b^3}{ab(3+b)}$ | |
$\dfrac{ab^2+9b−3ab+12b−b^2}{ab(3+b)}$ | |
$\dfrac{a^2b−9a−3ab+12b+b^2−b^3}{ab(3+b)}$ |
Question 9 Explanation:
The correct answer is (E). As with any expressions involving combining fractions, we first need to find a common denominator to perform any simplifying. We can see that we have denominators of:
$3 + b$, $b$, and $a$, so:
$ \left( \frac{a}{3+b}*\frac{a}{a}*\frac{b}{b} \right) $ $ -\left(\frac{3}{b}*\frac{3+b}{3+b}*\frac{a}{a} \right) $ $ +\left(\frac{4-b}{a}*\frac{b}{b}*\frac{3+b}{3+b} \right)$
We will now have a common denominator of $ab(3 + b$) and need only to simplify our numerator to arrive at the answer:
$a^2b-3a(3+b) $ $ + \, b(4-b)(3+b)$
$ \to a^2b-9a-3ab $ $ + \, b(12+4b-3b-b^2)$
$ \to a^2b-9a-3ab $ $ + \, 12b+b^2-b^3$
We can see that this is the same numerator as answer (E).
$3 + b$, $b$, and $a$, so:
$ \left( \frac{a}{3+b}*\frac{a}{a}*\frac{b}{b} \right) $ $ -\left(\frac{3}{b}*\frac{3+b}{3+b}*\frac{a}{a} \right) $ $ +\left(\frac{4-b}{a}*\frac{b}{b}*\frac{3+b}{3+b} \right)$
We will now have a common denominator of $ab(3 + b$) and need only to simplify our numerator to arrive at the answer:
$a^2b-3a(3+b) $ $ + \, b(4-b)(3+b)$
$ \to a^2b-9a-3ab $ $ + \, b(12+4b-3b-b^2)$
$ \to a^2b-9a-3ab $ $ + \, 12b+b^2-b^3$
We can see that this is the same numerator as answer (E).
Question 10 |
What are the x-intercepts of the function below?
$f(x) = x^3 + 3x^2 − x − 3$
$− 3, − 1, 1$ | |
$− 3, 0, 1$ | |
$−i , i, 3$ | |
$0, 3$ | |
$− 3, 0$ |
Question 10 Explanation:
The correct answer is (A). Recall that the x-intercept of a function is where the function output $f(x) = 0$. So we begin by setting our function equal to 0 and solving for the target variable $x$:
$f(x) = 0 = x^3 + 3x^2 − x − 3$
The problem here is that we are most familiar with solving for $x$ when given a linear or a quadratic function and may not easily recall how to factor polynomials of degree 3. However, with some rearranging of terms, we may get a better idea of how to proceed:
$(x^3+ 3x^2) + (−x − 3)$
$→ x^2(x + 3) − 1(x + 3)$
$→ (x + 3)(x^2 − 1) = 0$
By grouping our terms together we can find commonalities to factor out to finally arrive at an expression that enables us to directly solve for $x$. Setting each of the parentheses equal to 0:
$x + 3 = 0, x^2 − 1 = 0$
$→ x = −3, x = −1, x = 1$
Recall that $x^2 − 1$ is a difference of squares.
Alternatively, if ‘$a$’ is a root of a polynomial function, then $f(a) = 0$. We can plug the answer choices into the function to see which answer choice has three values that all yield zero when plugged into the function. Only answer choice (A) works.
$f(x) = 0 = x^3 + 3x^2 − x − 3$
The problem here is that we are most familiar with solving for $x$ when given a linear or a quadratic function and may not easily recall how to factor polynomials of degree 3. However, with some rearranging of terms, we may get a better idea of how to proceed:
$(x^3+ 3x^2) + (−x − 3)$
$→ x^2(x + 3) − 1(x + 3)$
$→ (x + 3)(x^2 − 1) = 0$
By grouping our terms together we can find commonalities to factor out to finally arrive at an expression that enables us to directly solve for $x$. Setting each of the parentheses equal to 0:
$x + 3 = 0, x^2 − 1 = 0$
$→ x = −3, x = −1, x = 1$
Recall that $x^2 − 1$ is a difference of squares.
Alternatively, if ‘$a$’ is a root of a polynomial function, then $f(a) = 0$. We can plug the answer choices into the function to see which answer choice has three values that all yield zero when plugged into the function. Only answer choice (A) works.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
More Practice Tests:
ACT Main Menu >>
ACT Math Practice >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
