This is the fourth and final free SAT Math practice test that we offer at High School Test Prep. It is also our most challenging test, with a variety of difficult and very difficult questions. The topics covered by these questions all fall under the SAT Math category that is called Passport to Advanced Math.
The use of a calculator is allowed. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In a recent survey of two popular best-selling books, two-fifths of the 2,200 polled said they did not enjoy the second book, but did enjoy the first book. Of those, 40% were adults over 18. If three-eighths of those surveyed were adults over 18, how many adults over 18 did NOT report that they enjoyed the first book but not the second book?
187 | |
352 | |
473 | |
626 |
Question 1 Explanation:
Remember to find each category separately to keep the different numbers clear. The total number of people was 2,200.
$\frac{2}{5}$ of 2,200 = 880, so 880 of those surveyed said they did not enjoy the second book, but enjoyed the first book. Of these 880 people, 40% were adults over 18, so in this group there were 880 * 0.4 = 352 people.
It is also stated that $\frac{3}{8}$ of the 2,200 surveyed, or 825 people who are adults over 18. To find the number of adults who did not report that they enjoyed the first book but not the second, subtract the portion who did report they enjoyed the first book but not the second from the total number of adults:
825 − 352 = 473 adults.
$\frac{2}{5}$ of 2,200 = 880, so 880 of those surveyed said they did not enjoy the second book, but enjoyed the first book. Of these 880 people, 40% were adults over 18, so in this group there were 880 * 0.4 = 352 people.
It is also stated that $\frac{3}{8}$ of the 2,200 surveyed, or 825 people who are adults over 18. To find the number of adults who did not report that they enjoyed the first book but not the second, subtract the portion who did report they enjoyed the first book but not the second from the total number of adults:
825 − 352 = 473 adults.
Question 2 |
The diameter of a circle is increased by 80%. By what percent is the area increased?
80% | |
224% | |
180% | |
325% |
Question 2 Explanation:
This is a great question for plugging in your own values. Let’s say the value of the original diameter was 10. The original area would be:
$\text{area} = π\,r^2$
$\text{area} = (5)^2π$
$\text{area} = 25π$
If the diameter increased by 80%, the new diameter would be 18, and the new area would be:
$\text{area} = π\,r^2$
$\text{area} = (9)^2π$
$\text{area} =81π$
The formula for percentage increase is:
$\frac{\text{New Value } − \text{ Original Value}}{\text{Original Value}}$ $\ast 100$
The numerator is: $81π − 25π = 56π$
$\dfrac{56π}{25π} * 100 = 224\%$
$\text{area} = π\,r^2$
$\text{area} = (5)^2π$
$\text{area} = 25π$
If the diameter increased by 80%, the new diameter would be 18, and the new area would be:
$\text{area} = π\,r^2$
$\text{area} = (9)^2π$
$\text{area} =81π$
The formula for percentage increase is:
$\frac{\text{New Value } − \text{ Original Value}}{\text{Original Value}}$ $\ast 100$
The numerator is: $81π − 25π = 56π$
$\dfrac{56π}{25π} * 100 = 224\%$
Question 3 |
For triangle $ABC$ shown below, what is its area rounded to the nearest tenth?
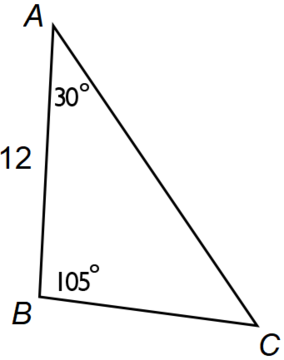
49.2 | |
36.0 | |
41.6 | |
72.0 |
Question 3 Explanation:
The key to "unlocking" the problem is to realize that if a "vertical" is dropped from point $B$ to $D$ we end up creating a $30-60-90$ triangle and a $45-45-90$ triangle.
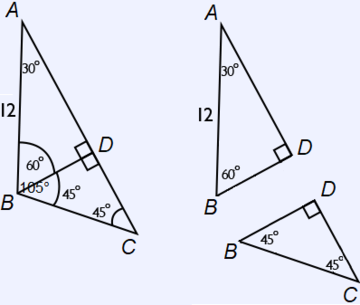
Using the properties of $30-60-90$ triangles, we know that $BD$ will be half the length of $AB$, or $6$, and we know that $AD$ will be $6\sqrt{3}$.
Using the properties of $45-45-90$ triangles, we know that $CD = BD = 6$.
Area of triangle $ABC =$ area of triangle $ABD$ + area of triangle $BCD$
$= 18\sqrt{3} + 18$
$≈ 49.2$

Using the properties of $30-60-90$ triangles, we know that $BD$ will be half the length of $AB$, or $6$, and we know that $AD$ will be $6\sqrt{3}$.
Using the properties of $45-45-90$ triangles, we know that $CD = BD = 6$.
Area of triangle $ABC =$ area of triangle $ABD$ + area of triangle $BCD$
$= 18\sqrt{3} + 18$
$≈ 49.2$
Question 4 |
A passenger ship left Southampton, England for the Moroccan coast. The ship travelled the first 230 miles at an average speed of 20 knots, then increased its speed for the next 345 miles to 30 knots. It travelled the remaining 598 miles at an average speed of 40 knots. What was the ship’s approximate average speed in miles per hour? (1 knot = 1.15 miles per hour)
36 | |
38 | |
40 | |
42 |
Question 4 Explanation:
In order to calculate the average speed of the trip, it is first necessary to solve for the total number of miles traveled and the total length of time traveled. Because the question asks for the average speed in miles per hour (and not knots), it is also necessary to convert all knots into miles per hour (mph).
Use the provided unit conversion to set up a general expression relating knots to mph:
$\frac{1 \text{ knot}}{1.15 \text{ miles}}$ $= \frac{y \text { knots}}{x \text{ miles}}$
where $y$ = 20, 30, and 40:
$\frac{1 \text{ knot}}{1.15 \text{ miles}}$ $= \frac{20 \text{ knots}}{x \text{ miles}}$
Solving for $x$:
$x \text{ mph}$ $= 20 \text{ knots} \ast \frac{1.15 \text{ mph}}{1 \text{ knot}}$ $= 23 \text{ mph}$
Notice that knots cancel from the numerator and denominator leaving units of mph, which is what we are looking for; this verifies that we are on the right track towards the solution. Repeat this calculation for the other knot values to find: 30 knots = 34.5 mph; 40 knots = 46 mph.
Using the calculated mph values, we can now solve for the length of time each portion of the trip took. Recall that a total distance travelled is equal to a rate, or speed of travel, multiplied with a length of time; or:
$\text{Distance} = \text{Rate} \ast \text{Time}$
Dimensional analysis is again useful to verify that the equation results in the appropriate units.
Use the distances and corresponding rates to solve for each time:
$230 \text{ miles}$ $= \frac{23 \text{ miles}}{\text{hours}} \ast \text{time}$
$230 \text{ miles} \ast \frac{\text{hours}}{23 \text{ miles}}$ $= 10 \text{ hours}$
Repeat this calculation for the other times: 345 miles takes 10 hours, and 598 miles takes 13 hours.
Use the calculated values to divide the total distance traveled by the total length of time traveled to determine the overall average rate of travel:
Avg speed $=$ $\frac{230 + 345 + 598 \text{ miles}}{10 + 10 + 13 \text{ hours}}$
$=$ $\frac{1173 \text{ miles}}{33 \text{ hours}}$
$≈ 35.55 \frac{\text{miles}}{\text{hour}}$, which is approximately 36 mph.
Use the provided unit conversion to set up a general expression relating knots to mph:
$\frac{1 \text{ knot}}{1.15 \text{ miles}}$ $= \frac{y \text { knots}}{x \text{ miles}}$
where $y$ = 20, 30, and 40:
$\frac{1 \text{ knot}}{1.15 \text{ miles}}$ $= \frac{20 \text{ knots}}{x \text{ miles}}$
Solving for $x$:
$x \text{ mph}$ $= 20 \text{ knots} \ast \frac{1.15 \text{ mph}}{1 \text{ knot}}$ $= 23 \text{ mph}$
Notice that knots cancel from the numerator and denominator leaving units of mph, which is what we are looking for; this verifies that we are on the right track towards the solution. Repeat this calculation for the other knot values to find: 30 knots = 34.5 mph; 40 knots = 46 mph.
Using the calculated mph values, we can now solve for the length of time each portion of the trip took. Recall that a total distance travelled is equal to a rate, or speed of travel, multiplied with a length of time; or:
$\text{Distance} = \text{Rate} \ast \text{Time}$
Dimensional analysis is again useful to verify that the equation results in the appropriate units.
Use the distances and corresponding rates to solve for each time:
$230 \text{ miles}$ $= \frac{23 \text{ miles}}{\text{hours}} \ast \text{time}$
$230 \text{ miles} \ast \frac{\text{hours}}{23 \text{ miles}}$ $= 10 \text{ hours}$
Repeat this calculation for the other times: 345 miles takes 10 hours, and 598 miles takes 13 hours.
Use the calculated values to divide the total distance traveled by the total length of time traveled to determine the overall average rate of travel:
Avg speed $=$ $\frac{230 + 345 + 598 \text{ miles}}{10 + 10 + 13 \text{ hours}}$
$=$ $\frac{1173 \text{ miles}}{33 \text{ hours}}$
$≈ 35.55 \frac{\text{miles}}{\text{hour}}$, which is approximately 36 mph.
Question 5 |
The initial number of elements in Set A is x, where x > 0. If the number of elements in Set A doubles every hour, which of the following represents the increase in the number of elements in Set A after exactly one day?
23x23 | |
(223)x | |
23x24 | |
(224)x − x |
Question 5 Explanation:
To find the increase in the elements, we need to subtract the original number from the final total number. Since the original amount is going to be multiplied by 2 (or doubled) 24 times, we can express this as 224 — after 1 hr we have 21 * x, after 2 hrs we have 22 * x, after 3 hrs we have 23 * x, and after 24 hours we have 224 * x.
Thus, the final total increase will be 224x (the final total) − x (the original number).
Thus, the final total increase will be 224x (the final total) − x (the original number).
Question 6 |
At a certain lab, the current ratio of scientists to engineers is 5:1. The lab is considering a plan where 75 new team members would be hired in the ratio of two engineers per scientist, which would change the ratio of scientists to engineers to approximately 2:3. Approximately how many scientists currently work at the lab?
5 | |
10 | |
15 | |
20 |
Question 6 Explanation:
Currently our ratio is: $\frac{S}{E} = \frac{5}{1}$, or 5E = S
Out of the 75 hires, for every three hires two will be engineers, and one will be a scientist. That will add 50 engineers and 25 scientists. We’re told that adding these people to the mix creates a new ratio:
$\frac{(E + 50)}{(S + 25)}$ $=$ $\frac{3}{2}$
Substitute 5E for S, and solve:
$\frac{(E + 50)}{(5E + 25)}$ $=$ $\frac{3}{2}$
2(E + 50) = 3(5E + 25)
2E + 100 = 15E + 75
100 = 15E + 75
25 = 15E
$\frac{25}{13}$ = E
1.9 = E (or approximately 2)
Since there are currently 5 scientists for every engineer, then there are approximately 10 scientists.
Out of the 75 hires, for every three hires two will be engineers, and one will be a scientist. That will add 50 engineers and 25 scientists. We’re told that adding these people to the mix creates a new ratio:
$\frac{(E + 50)}{(S + 25)}$ $=$ $\frac{3}{2}$
Substitute 5E for S, and solve:
$\frac{(E + 50)}{(5E + 25)}$ $=$ $\frac{3}{2}$
2(E + 50) = 3(5E + 25)
2E + 100 = 15E + 75
100 = 15E + 75
25 = 15E
$\frac{25}{13}$ = E
1.9 = E (or approximately 2)
Since there are currently 5 scientists for every engineer, then there are approximately 10 scientists.
Question 7 |
On a number line with points LMNOP, the ratio of LM to MN is 1, and the ratio of NO to OP is 3/4. If the length of LP is 28 and the length of MO is 13, what is the ratio of LO to MP?
$\dfrac{7}{18}$
| |
$\dfrac{13}{28}$
| |
$\dfrac{15}{28}$
| |
$\dfrac{20}{21}$
|
Question 7 Explanation:
Let’s draw the number line:
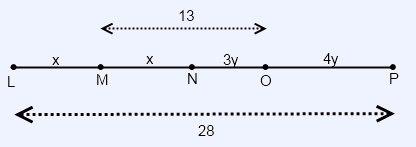
Let's choose the variables $x$ and $y$ to help express the ratios. Right now the ratio of LO to MP is $\dfrac{2x + 3y}{x + 7y}$
If we could find the values of $x$ and $y$, then we could determine the ratio.
We can set up 2 equations based on the given information:
Equation for MO: $x + 3y = 13$
Equation for LP: $2x + 7y = 28$
We can solve Eq. #1 for $x$:
$x = 13 – 3y$
Substitute this value of $x$ into Eq. #2:
$2(13 – 3y) + 7y = 28$
$26 – 6y + 7y = 28$
$26 + y = 28$
$y = 2$
Now we can find $x$:
$x + 3(2) = 13$
$x + 6 = 13$
$x = 7$
Now plug in the values of $x = 7$ and $y = 2$ to find the ratio:
= $\dfrac{2x + 3y}{x + 7y}$
= $\dfrac{14 + 6}{7 + 14}$
= $\dfrac{20}{21}$

Let's choose the variables $x$ and $y$ to help express the ratios. Right now the ratio of LO to MP is $\dfrac{2x + 3y}{x + 7y}$
If we could find the values of $x$ and $y$, then we could determine the ratio.
We can set up 2 equations based on the given information:
Equation for MO: $x + 3y = 13$
Equation for LP: $2x + 7y = 28$
We can solve Eq. #1 for $x$:
$x = 13 – 3y$
Substitute this value of $x$ into Eq. #2:
$2(13 – 3y) + 7y = 28$
$26 – 6y + 7y = 28$
$26 + y = 28$
$y = 2$
Now we can find $x$:
$x + 3(2) = 13$
$x + 6 = 13$
$x = 7$
Now plug in the values of $x = 7$ and $y = 2$ to find the ratio:
= $\dfrac{2x + 3y}{x + 7y}$
= $\dfrac{14 + 6}{7 + 14}$
= $\dfrac{20}{21}$
Question 8 |
In the $xy$-coordinate plane, a circle with center $(−4, 0)$ is tangent to the line $y = −x$. What is the circumference of the circle?
$4\pi$ | |
$2\pi \sqrt{2}$ | |
$4\pi$ | |
$4\pi \sqrt{2}$ |
Question 8 Explanation:
Start by drawing a diagram to better visualize the problem:
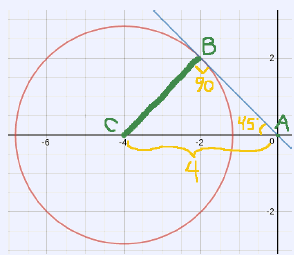
The line $y = −x$ makes a 45° angle with each axis in the second quadrant. Connect the center of the circle (Point C) to the point of tangency on $y = −x$ (Point B). The radius of a circle (BC) is perpendicular to its point of tangency. Point A is at the origin (0,0).
We have 45° between AB and the x-axis and 90° between BC and AB. Since the angles of a triangle sum to 180°, we know angle BCA must be 45°. Triangle ABC is a 45°–45°–90° triangle.
The length of AC = 4. Because Triangle ABC is a 45°-45°-90° triangle, we can use our knowledge of special right triangle ratios to show that:
$AC = BC * \sqrt{2}$, or $BC = \frac{AC}{\sqrt{2}}$
Thus, radius $BC = \frac{4}{\sqrt{2}} = 2\sqrt{2}$
Circumference $= 2 \pi r$
$= 2 \pi * 2 \sqrt{2} = 4\pi \sqrt{2}$

The line $y = −x$ makes a 45° angle with each axis in the second quadrant. Connect the center of the circle (Point C) to the point of tangency on $y = −x$ (Point B). The radius of a circle (BC) is perpendicular to its point of tangency. Point A is at the origin (0,0).
We have 45° between AB and the x-axis and 90° between BC and AB. Since the angles of a triangle sum to 180°, we know angle BCA must be 45°. Triangle ABC is a 45°–45°–90° triangle.
The length of AC = 4. Because Triangle ABC is a 45°-45°-90° triangle, we can use our knowledge of special right triangle ratios to show that:
$AC = BC * \sqrt{2}$, or $BC = \frac{AC}{\sqrt{2}}$
Thus, radius $BC = \frac{4}{\sqrt{2}} = 2\sqrt{2}$
Circumference $= 2 \pi r$
$= 2 \pi * 2 \sqrt{2} = 4\pi \sqrt{2}$
Question 9 |
Consider two parallel lines $F$ and $G$ shown below. Line $F$ forms an angle of $60°$ with the $x$-axis. Line $G$ has a $y$-intercept of $−3$. What is the shortest distance between the two parallel lines?

$3$ | |
$\sqrt{3}$ | |
$\dfrac{3\sqrt{3}}{2}$ | |
$\dfrac{3}{2}$ |
Question 9 Explanation:
Line $G$ has a $y$-intercept of $−3$. $OA = 3$.
Since $F$ makes an angle of $60°$ with the $x$-axis, it must make an angle of $30°$ with the $y$-axis.
Because $G$ is parallel to $F$, it too must make an angle of $30°$ with the $y$-axis.
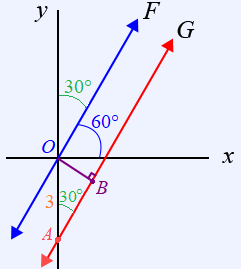
The shortest distance between two parallel lines will always be perpendicular.
By adding line $OB$ to our sketch, we can form a $30-60-90$ triangle, $OAB$.
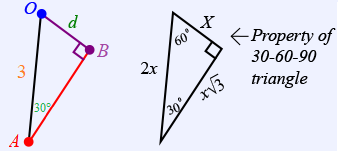
We can find the shortest distance, $OB = d$, using properties of $30-60-90$ triangles. Because $OB$ is opposite the $30°$ it will be the shortest side, which is half the hypotenuse. Thus, $d = \frac{3}{2}$.
Since $F$ makes an angle of $60°$ with the $x$-axis, it must make an angle of $30°$ with the $y$-axis.
Because $G$ is parallel to $F$, it too must make an angle of $30°$ with the $y$-axis.

The shortest distance between two parallel lines will always be perpendicular.
By adding line $OB$ to our sketch, we can form a $30-60-90$ triangle, $OAB$.
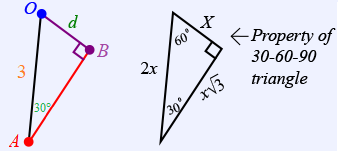
We can find the shortest distance, $OB = d$, using properties of $30-60-90$ triangles. Because $OB$ is opposite the $30°$ it will be the shortest side, which is half the hypotenuse. Thus, $d = \frac{3}{2}$.
Question 10 |
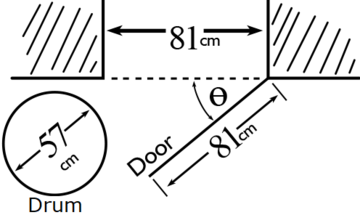
The illustration above shows a cylindrical drum with a diameter of $57$ cm, a door with a length of $81$ cm, and an opening that is $81$ cm across. What is the minimum angle, $Θ$, that the door must be opened to allow the drum to pass through the opening (ignoring the thickness of the door)?
50° | |
35° | |
30° | |
45° |
Question 10 Explanation:
Refer to the illustration below.
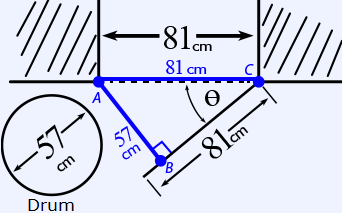
The key to unlocking this problem is to recognize that the shortest distance (most restrictive) between Point $A$ and Point $B$ occurs when $AB$ (“the opening”) is perpendicular to $BC$ (“the door”). Thus, for the drum to fit, $AB$ must be a minimum of $57$ cm.
We now have a right triangle, $ABC$, with hypotenuse $AC = 81$ cm and the opposite leg (of $Θ$) $AB = 57$ cm.
We can now use the trigonometric ratio, $\sin Θ = \dfrac{\text{Opposite}}{\text{Hypotenuse}}$, to solve for $Θ$.
$\sin Θ = \dfrac{\text{Opposite}}{\text{Hypotenuse}}$
$\sin Θ = \dfrac{57}{81}$
$Θ = \arcsin\left(\dfrac{57}{81}\right)$
$Θ = 45°$

The key to unlocking this problem is to recognize that the shortest distance (most restrictive) between Point $A$ and Point $B$ occurs when $AB$ (“the opening”) is perpendicular to $BC$ (“the door”). Thus, for the drum to fit, $AB$ must be a minimum of $57$ cm.
We now have a right triangle, $ABC$, with hypotenuse $AC = 81$ cm and the opposite leg (of $Θ$) $AB = 57$ cm.
We can now use the trigonometric ratio, $\sin Θ = \dfrac{\text{Opposite}}{\text{Hypotenuse}}$, to solve for $Θ$.
$\sin Θ = \dfrac{\text{Opposite}}{\text{Hypotenuse}}$
$\sin Θ = \dfrac{57}{81}$
$Θ = \arcsin\left(\dfrac{57}{81}\right)$
$Θ = 45°$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
More Practice Tests:
More SAT Math >>
SAT Main Menu >>
