Below is our most difficult set of SAT Math—No Calculator practice questions. This should give you a good idea of the what the most challenging SAT math problems are like. As with all of our free practice questions, detailed explanations are provided. Good luck!
The use of a calculator is NOT permitted. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The average of several exam scores is 80. One make-up exam was given. Included with the other scores, the new average was 84. If the score on the make-up exam was 92, how many total exams were given?
2 | |
3 | |
4 | |
5 |
Question 1 Explanation:
Recall that average is calculated by adding a group of numbers and then dividing by the count of those numbers. Plugging in what we’re given to the formula for average:
$80 = \frac{\text{Sum}}{x}$
$80x = \text{Sum}$
$84 = \frac{(\text{Sum } + \text{ Makeup Score})}{(x \, + \, 1)}$
Multiplying both sides by $x + 1$:
$84x + 84 = \text{Sum }$ $+ \text{ Makeup Score}$
Let’s substitute $80x$ for Sum:
$84x + 84 = 80x$ $+ \text{ Makeup Score}$
$4x + 84 = \text{ Makeup Score}$
We are told that the makeup score was $92$:
$4x + 84 = 92$
$4x = 8$
$x = 2$
The question asks for the total number of exams, which is $x+1 = 3$
$80 = \frac{\text{Sum}}{x}$
$80x = \text{Sum}$
$84 = \frac{(\text{Sum } + \text{ Makeup Score})}{(x \, + \, 1)}$
Multiplying both sides by $x + 1$:
$84x + 84 = \text{Sum }$ $+ \text{ Makeup Score}$
Let’s substitute $80x$ for Sum:
$84x + 84 = 80x$ $+ \text{ Makeup Score}$
$4x + 84 = \text{ Makeup Score}$
We are told that the makeup score was $92$:
$4x + 84 = 92$
$4x = 8$
$x = 2$
The question asks for the total number of exams, which is $x+1 = 3$
Question 2 |
The midpoints of the sides of a square are connected to form a new inscribed square. How many times greater than the area of the inscribed square is the area of the original square?
$\dfrac{1}{2}$ | |
$2$ | |
$8$ | |
$8\sqrt{2}$ |
Question 2 Explanation:

This is a great question to pick numbers for, especially since the correct answer is a ratio. Let’s say the length of the original square is 4. The midpoint divides the sides into two halves, each with a value of 2. The isosceles triangles formed by the lines connecting the midpoints are 45°, 45,° and 90° special right triangles. Therefore the hypotenuse of those triangles would be:
$2\sqrt{2}$
The area of the original square is:
$4 * 4 = 16$
The area of the inscribed square is:
$2\sqrt{2} * 2\sqrt{2} = 4 * 2 = 8$
The original square’s area is $2x$ greater than the inscribed square’s area.
Question 3 |
Shauna is throwing a bachelorette party for her best friend with $x$ guests total. All of the guests plan to split the cost of renting a limo for $y$ dollars. The day before, $z$ guests cancel. Which of the following represents the percent increase in the amount each guest must pay towards the limo rental?
$\dfrac{y}{x}$ | |
$\dfrac{y (x − z)}{z − x}$ | |
$\dfrac{100yz }{ y(x − z)}$ | |
$\dfrac{100x }{ y (z − x)}$ |
Question 3 Explanation:
This is a great question to pick numbers. Let’s choose easy, manageable values. If $x = 5$ and $y = 10$, then each guest would originally have paid $\frac{10}{5}$ = $\$2$.
Let’s say $z = 3$. Now with only $2$ guests, each will pay $\$5$.
The percent change is always the change over the original amount: $\frac{5 − 2}{2}$ = $\frac{3}{2}$ = $150\%$.
Now we’ll plug in our picked numbers into the answer choices to see which one yields the same percent increase.
(A) $\dfrac{10}{5}$ = $2$
(B) $\dfrac{10 (5 − 3) }{ 3 − 5 }$= $\dfrac{20}{−2}$ = $−10$
(C) $\dfrac{100(10)(3) }{ 10(5 − 3)}$ = $\dfrac{3000}{20}$ = $150$ ⇒ Correct!
(D) $\dfrac{100(5) }{ 10(3 − 5)}$ = $\dfrac{500}{−20}$= $−25$
Let’s say $z = 3$. Now with only $2$ guests, each will pay $\$5$.
The percent change is always the change over the original amount: $\frac{5 − 2}{2}$ = $\frac{3}{2}$ = $150\%$.
Now we’ll plug in our picked numbers into the answer choices to see which one yields the same percent increase.
(A) $\dfrac{10}{5}$ = $2$
(B) $\dfrac{10 (5 − 3) }{ 3 − 5 }$= $\dfrac{20}{−2}$ = $−10$
(C) $\dfrac{100(10)(3) }{ 10(5 − 3)}$ = $\dfrac{3000}{20}$ = $150$ ⇒ Correct!
(D) $\dfrac{100(5) }{ 10(3 − 5)}$ = $\dfrac{500}{−20}$= $−25$
Question 4 |
For all negative integers m other than −1, let ⏀m⏀ be defined as the product of all the negative odd integers greater than m. What is the value of :
$\dfrac{⏀(-85)⏀}{⏀(-84)⏀}$
−85 | |
−84 | |
−83 | |
1 |
Question 4 Explanation:
For a function question using symbols, we must carefully apply the described rule of the symbol to the given values.
⏀−85⏀ is defined as the product of ALL the negative odd integers GREATER than −85.
So, ⏀−85⏀ = −83 * −81 * −79 * −77… −5 * −3 * −1
Likewise, ⏀−84⏀ = −83 * −81 * −79 * −77… −5 * −3 * −1
When these numbers are divided, we can see that every value will cancel out. The answer is 1.
⏀−85⏀ is defined as the product of ALL the negative odd integers GREATER than −85.
So, ⏀−85⏀ = −83 * −81 * −79 * −77… −5 * −3 * −1
Likewise, ⏀−84⏀ = −83 * −81 * −79 * −77… −5 * −3 * −1
When these numbers are divided, we can see that every value will cancel out. The answer is 1.
Question 5 |
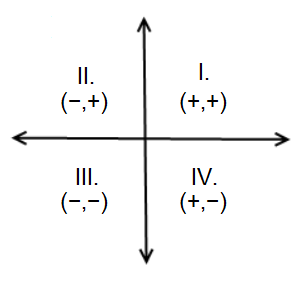
If the product of $x$ and $y$ does not equal zero, which of the following could be true based on the figure above?
I. ($−x, y$) lies above the x-axis and to the right of the y-axis.
II. ($x, −y$) lies below the x-axis and to the left of the y-axis.
III. ($x, y$) lies on the x-axis to the right of the y-axis.
I only | |
II only | |
I and II | |
II and III |
Question 5 Explanation:
“The product of $x$ and $y$ does not equal zero” means that both $x$ and $y$ must be non-zero numbers, but otherwise there is no restriction. Only Choice III describes a situation where one of the numbers is zero; “lies on the x-axis” implies that $y$ = zero which is not permitted. Choices I and II are fine since $x$ and $y$ are non-zero numbers — i.e. neither lies on the axes. Therefore, Answer (C) is the correct answer.
Question 6 |
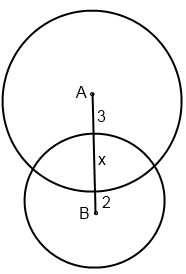
In the figure, the radius of circle B is three-fourths the radius of circle A. The distance from center A to the circumference of circle B is 3, and the distance from center B to the circumference of circle A is 2. What is the area of the smaller circle?
$π$ | |
$3π$ | |
$6π$ | |
$9π$ |
Question 6 Explanation:
To find the area of the smaller circle (Circle B), we’ll need to find the radius of circle B.
The radius of circle B is $2 + x$.
We’re told that the radius of B is three-fourths the radius of A, so we can set up a proportion:
$\dfrac{3}{4} * (3 + x) = 2 + x$
Solving, we get:
$\dfrac{9}{4} + \dfrac{3*x}{4} = 2 + x$
$\dfrac{1}{4} + \dfrac{3x}{4} = x$
$\dfrac{1}{4} = \dfrac{x}{4}$
$1 = x$
If $x = 1$, the radius of circle B is: $2 + 1 = 3$
The area will be: $πr^2 = 9π$
We’re told that the radius of B is three-fourths the radius of A, so we can set up a proportion:
$\dfrac{3}{4} * (3 + x) = 2 + x$
Solving, we get:
$\dfrac{9}{4} + \dfrac{3*x}{4} = 2 + x$
$\dfrac{1}{4} + \dfrac{3x}{4} = x$
$\dfrac{1}{4} = \dfrac{x}{4}$
$1 = x$
If $x = 1$, the radius of circle B is: $2 + 1 = 3$
The area will be: $πr^2 = 9π$
Question 7 |
If Eric was 22 years old $x$ years ago and Shelley will be 24 years old in $y$ years, what was the average of their ages 4 years ago?
$\dfrac{x + y}{2}$ | |
$\dfrac{y + 38}{3}$ | |
$\dfrac{x − y + 28}{4}$ | |
$\dfrac{x − y + 38}{2}$ |
Question 7 Explanation:
The problem asks for the average of the ages of 2 people. Thus, the divisor will be 2, and answer choices (B) and (C) can be eliminated. That leaves us with just (A) and (D).
Let's start off by converting the problem into mathematical expressions. If Eric was 22 years old $x$ years ago, then he is currently:
$22 + x \text{ Years Old}$
If Shelley will be 24 years old in $y$ years, then she is currently:
$24 − y \text{ Years Old}$
(If these expressions seem confusing to you, try plugging in some numbers to convince yourself that they hold true.)
This means, that 4 years ago, Eric was:
$x + 22 − 4$ $= x + 18 \text{ Years Old}$
Likewise, 4 years ago, Shelley was:
$24 − y − 4$ $= 20 − y \text{ Years Old}$
Taking the average of these two ages, we get:
$\dfrac{x + 18 + 20 - y}{2}$ $= \dfrac{x - y + 38}{2}$
Let's start off by converting the problem into mathematical expressions. If Eric was 22 years old $x$ years ago, then he is currently:
$22 + x \text{ Years Old}$
If Shelley will be 24 years old in $y$ years, then she is currently:
$24 − y \text{ Years Old}$
(If these expressions seem confusing to you, try plugging in some numbers to convince yourself that they hold true.)
This means, that 4 years ago, Eric was:
$x + 22 − 4$ $= x + 18 \text{ Years Old}$
Likewise, 4 years ago, Shelley was:
$24 − y − 4$ $= 20 − y \text{ Years Old}$
Taking the average of these two ages, we get:
$\dfrac{x + 18 + 20 - y}{2}$ $= \dfrac{x - y + 38}{2}$
Question 8 |
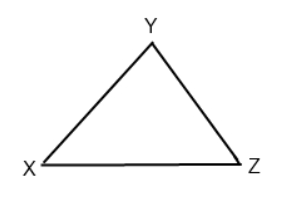
Point A lies between X and Y. Point B lies on YZ and Point C lies on XZ. BZ is congruent to CZ, and ∠XYZ = 90°. XZ – CZ = XA. What is the value of ∠ACB?
45° | |
60° | |
75° | |
90° |
Question 8 Explanation:
This is a Geometry question, so you’ll want to begin by drawing the figure on your own and filling in the given information. Let’s label $∠ACB$ as $z$ to keep track of it.
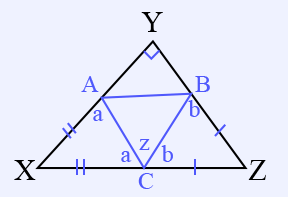
The problem tells us that $BZ$ and $CZ$ are congruent. Thus, $∠ZBC$ and $∠ZCB$ (denoted by $b$ for simplicity) are equal.
The problem tells us that $XZ − CZ = XA$. Looking at the triangle, we can also see that $XZ − CZ = XC$. Hence, sides $XC$ and $XA$ are equal, and so are the angles opposite them (denoted by $a$.)
Because $a, z,$ and $b$ are supplementary, $a + b + z = 180$
This is our First Equation.
Let's look at our Second Equation:
We know that $∠X + ∠Y + ∠Z = 180°$
Simplifying, we get:
$∠X + 90° + ∠Z = 180°$
$∠X + ∠Z = 90°$
We also know that $∠X = 180 − 2a$ and $∠Z = 180 − 2b$
Substituting these values, we get:
$(180 − 2a) + (180 − 2b)$ $= 90$
Simplifying our Second Equation:
$360 − 2a − 2b = 90$
Subtracting $360$:
$−2a − 2b = −270$ $→ 270 = 2a + 2b$
Let’s factor out the 2 from the variables:
$270 = 2(a + b)$
Now, let's go back to the First Equation. If we manipulate it, we can see that $a + b = 180 − z.$ Let’s substitute $180 − z$ for $a + b$:
$270 = 2(180 − z)$
$z = 45° = ∠ACB$

The problem tells us that $BZ$ and $CZ$ are congruent. Thus, $∠ZBC$ and $∠ZCB$ (denoted by $b$ for simplicity) are equal.
The problem tells us that $XZ − CZ = XA$. Looking at the triangle, we can also see that $XZ − CZ = XC$. Hence, sides $XC$ and $XA$ are equal, and so are the angles opposite them (denoted by $a$.)
Because $a, z,$ and $b$ are supplementary, $a + b + z = 180$
This is our First Equation.
Let's look at our Second Equation:
We know that $∠X + ∠Y + ∠Z = 180°$
Simplifying, we get:
$∠X + 90° + ∠Z = 180°$
$∠X + ∠Z = 90°$
We also know that $∠X = 180 − 2a$ and $∠Z = 180 − 2b$
Substituting these values, we get:
$(180 − 2a) + (180 − 2b)$ $= 90$
Simplifying our Second Equation:
$360 − 2a − 2b = 90$
Subtracting $360$:
$−2a − 2b = −270$ $→ 270 = 2a + 2b$
Let’s factor out the 2 from the variables:
$270 = 2(a + b)$
Now, let's go back to the First Equation. If we manipulate it, we can see that $a + b = 180 − z.$ Let’s substitute $180 − z$ for $a + b$:
$270 = 2(180 − z)$
$z = 45° = ∠ACB$
Question 9 |
The points A, B, and C lie on the same circle. If A=(3,13), B=(15,5), and C=(20,30), which of the following could be the center of the circle?
(15,18) | |
(16,17) | |
(15,13) | |
(17,15) |
Question 9 Explanation:
The distance from the center of the circle to each of the points, A, B, and C, on the circle must be the same. The distance between any two points can be found using the distance formula:
If we call the center of the circle ($h, k$), the distance formula becomes:
$Distance$ $= \sqrt{(x_2 - h)^2 + (y_2 - k)^2}$, where $x_2$ and $y_2$ will be the coordinates of A, B, and C
It is helpful to always keep your Pythagorean triples in mind; be on the lookout for 3–4–5 and 5–12–13 right triangles.
It is going to be quickest to work backwards. Let’s try answer choice (C), center = (15,13), first:
$Distance$ $= \sqrt{(x_2 - 15)^2 + (y_2 - 13)^2}$
$Distance~from~A~to~center$ $= \sqrt{(3 - 15)^2 + (13 - 13)^2}$ $= \sqrt{(-12)^2 + (0)^2}$ $=\sqrt{144} = 12$
$Distance~from~B~to~center$ $= \sqrt{(15 - 15)^2 + (5 - 13)^2}$ $= \sqrt{(0)^2 + (-8)^2}$ $=\sqrt{64} = 8$
We can stop here, since the Distances between each point and the center must be the same, and we already have a discrepancy. Eventually, we get to answer choice (A), center = (15,18):
$Distance~from~A~to~center$ $= \sqrt{(3 - 15)^2 + (13 - 18)^2}$ $= \sqrt{(-12)^2 + (5)^2}$ $=\sqrt{169} = 13$
$Distance~from~B~to~center$ $= \sqrt{(15 - 15)^2 + (5 - 18)^2}$ $= \sqrt{(0)^2 + (-13)^2}$ $=\sqrt{169} = 13$
$Distance~from~C~to~center$ $= \sqrt{(20 - 15)^2 + (30 - 18)^2}$ $= \sqrt{(5)^2 + (12)^2}$ $=\sqrt{169} = 13$
If we call the center of the circle ($h, k$), the distance formula becomes:
$Distance$ $= \sqrt{(x_2 - h)^2 + (y_2 - k)^2}$, where $x_2$ and $y_2$ will be the coordinates of A, B, and C
It is helpful to always keep your Pythagorean triples in mind; be on the lookout for 3–4–5 and 5–12–13 right triangles.
It is going to be quickest to work backwards. Let’s try answer choice (C), center = (15,13), first:
$Distance$ $= \sqrt{(x_2 - 15)^2 + (y_2 - 13)^2}$
$Distance~from~A~to~center$ $= \sqrt{(3 - 15)^2 + (13 - 13)^2}$ $= \sqrt{(-12)^2 + (0)^2}$ $=\sqrt{144} = 12$
$Distance~from~B~to~center$ $= \sqrt{(15 - 15)^2 + (5 - 13)^2}$ $= \sqrt{(0)^2 + (-8)^2}$ $=\sqrt{64} = 8$
We can stop here, since the Distances between each point and the center must be the same, and we already have a discrepancy. Eventually, we get to answer choice (A), center = (15,18):
$Distance~from~A~to~center$ $= \sqrt{(3 - 15)^2 + (13 - 18)^2}$ $= \sqrt{(-12)^2 + (5)^2}$ $=\sqrt{169} = 13$
$Distance~from~B~to~center$ $= \sqrt{(15 - 15)^2 + (5 - 18)^2}$ $= \sqrt{(0)^2 + (-13)^2}$ $=\sqrt{169} = 13$
$Distance~from~C~to~center$ $= \sqrt{(20 - 15)^2 + (30 - 18)^2}$ $= \sqrt{(5)^2 + (12)^2}$ $=\sqrt{169} = 13$
Question 10 |
$3x^2 + kx = −3$
What value of $k$ will result in exactly one solution to the equation?
9 | |
−6 | |
10 | |
−10 |
Question 10 Explanation:
Solutions to a quadratic equation are also called “roots.” We use the quadratic formula to find roots.
$Roots = \dfrac{-b±\sqrt{b^2 - 4ac}}{2a}$
$b^2-4ac$ is known as the discriminant. When it is zero, there will be only one root.
We need to solve: $b^2 - 4ac = 0$. Before we do so, we need to rearrange our original equation so that it is in standard form:
$3x^2 + kx = -3$
$3x^2 + kx + 3 = 0$
$a = 3, b = k, c = 3$
Substituting into $b^2 - 4ac = 0$ we have:
$(k)^2 - 4(3)(3) = 0$
Solving for $k$:
$(k)^2 =36$
$k = ±\sqrt{36}$
$k = ±6$
The other (slower) way to approach this problem would be to take each answer and work backwards until you found the value for $k$ which allowed the quadratic to be factored into two identical factors.
$Roots = \dfrac{-b±\sqrt{b^2 - 4ac}}{2a}$
$b^2-4ac$ is known as the discriminant. When it is zero, there will be only one root.
We need to solve: $b^2 - 4ac = 0$. Before we do so, we need to rearrange our original equation so that it is in standard form:
$3x^2 + kx = -3$
$3x^2 + kx + 3 = 0$
$a = 3, b = k, c = 3$
Substituting into $b^2 - 4ac = 0$ we have:
$(k)^2 - 4(3)(3) = 0$
Solving for $k$:
$(k)^2 =36$
$k = ±\sqrt{36}$
$k = ±6$
The other (slower) way to approach this problem would be to take each answer and work backwards until you found the value for $k$ which allowed the quadratic to be factored into two identical factors.
Question 11 |
The value of $a$ is chosen such that the product of $2 + 3i$ and $3 + ai$, where $i = \sqrt{–1}$, is a real number (i.e. not complex). What will this product be?
$\dfrac{27}{2}$ | |
$3$ | |
$\dfrac{39}{2}$ | |
$\dfrac{–9}{2}$ |
Question 11 Explanation:
Begin by "FOIL"-ing the two complex numbers.
$(2 + 3i)(3 + ai)$
$(2)(3) + (2)(ai) + (3i)(3)$ $+ \, (3i)(ai)$
$6 + 2ai + 91 + 3ai^2$
Since $i = \sqrt{−1}$, $i^2 = (\sqrt{−1})^2 = −1$
$6 + 2ai + 9i + 3a(−1)$
$6 + 2ai + 9i − 3a$
To be a real number, the imaginary terms must be eliminated. To do so, we need to find $a$ such that:
$2ai + 9i = 0$
$2ai = −9i$
$ai = \dfrac{−9}{2}i$
$a = \dfrac{−9}{2}$
Subsituting $a = \dfrac{−9}{2}$ back into our equation, we have:
$6 + 2ai + 9i − 3a$
$6 + 2\left(−\dfrac{9}{2}\right)i$ $+ \, 9i − 3\left(−\dfrac{9}{2}\right)$
$6 − 9i + 9i + \dfrac {27}{2}$
$6 + \dfrac{27}{2}$
$\dfrac{12}{2} + {27}{2}$
$\dfrac{39}{2}$
$(2 + 3i)(3 + ai)$
$(2)(3) + (2)(ai) + (3i)(3)$ $+ \, (3i)(ai)$
$6 + 2ai + 91 + 3ai^2$
Since $i = \sqrt{−1}$, $i^2 = (\sqrt{−1})^2 = −1$
$6 + 2ai + 9i + 3a(−1)$
$6 + 2ai + 9i − 3a$
To be a real number, the imaginary terms must be eliminated. To do so, we need to find $a$ such that:
$2ai + 9i = 0$
$2ai = −9i$
$ai = \dfrac{−9}{2}i$
$a = \dfrac{−9}{2}$
Subsituting $a = \dfrac{−9}{2}$ back into our equation, we have:
$6 + 2ai + 9i − 3a$
$6 + 2\left(−\dfrac{9}{2}\right)i$ $+ \, 9i − 3\left(−\dfrac{9}{2}\right)$
$6 − 9i + 9i + \dfrac {27}{2}$
$6 + \dfrac{27}{2}$
$\dfrac{12}{2} + {27}{2}$
$\dfrac{39}{2}$
Question 12 |
A restaurant offers two levels of sweet tea: Somewhat-Sweet (somewhat sweet) and Super-Sweet (very sweet). The Super-Sweet iced tea has a sugar concentration of $5\%$ by weight (e.g. $5$ grams of sugar per $100$ grams of tea).
To make the perfect iced tea, Pamela mixes $200$ mL of Somewhat-Sweet with $300$ mL of Super-Sweet to end up with an iced-tea that has a sugar concentration of $3.5\%$ by weight. If the tea weighs approximately $1$ gram per milliliter ($1$ g/mL), what is the concentration of the Somewhat-Sweet iced tea?
$1.25\%$ | |
$3.33\%$ | |
$2.00\%$ | |
$2.50\%$ |
Question 12 Explanation:
Sugar concentration (by weight) $= \frac{\text{Total Sugar (g)}}{\text{Total Tea (g)}}$
$200$ mL of Somewhat tea $= 200 \text{ g}$
$300$ mL of Super tea $= 300 \text{ g}$
Let $c$ represent the grams of sugar in $100 \text{ g}$ of Somewhat-Sweet tea.
Total Sugar $= (200 \text{ g of Somewhat})$ $\left(\frac{c \text{ g of Sugar}}{100 \text { g of Somewhat}}\right)$ $ + \, (300 \text{ g of Super})$ $\left(\frac{5 \text{ g of Sugar}}{100 \text{ g of Super}}\right)$
Total sugar $= 2c + 15 \text{ g}$ of Sugar
Total tea $= 500 \text{ g}$ of Pamela's "perfect" iced tea
Sugar concentration (by weight) $= \frac{2c \, + \, 15 \text{g of Sugar}}{500 \text{ g of Pamela's}}$
We know Pamela's "perfect" iced tea has a concentration of $3.5\%$.
$\frac{2c \, + \, 15}{500} = \frac{3.5 \text{ g of Sugar}}{100 \text{ g of Pamela's}}$
Solving for $c$ we get:
$c = 1.25$ g of sugar $= 1.25\%$ concentration
$200$ mL of Somewhat tea $= 200 \text{ g}$
$300$ mL of Super tea $= 300 \text{ g}$
Let $c$ represent the grams of sugar in $100 \text{ g}$ of Somewhat-Sweet tea.
Total Sugar $= (200 \text{ g of Somewhat})$ $\left(\frac{c \text{ g of Sugar}}{100 \text { g of Somewhat}}\right)$ $ + \, (300 \text{ g of Super})$ $\left(\frac{5 \text{ g of Sugar}}{100 \text{ g of Super}}\right)$
Total sugar $= 2c + 15 \text{ g}$ of Sugar
Total tea $= 500 \text{ g}$ of Pamela's "perfect" iced tea
Sugar concentration (by weight) $= \frac{2c \, + \, 15 \text{g of Sugar}}{500 \text{ g of Pamela's}}$
We know Pamela's "perfect" iced tea has a concentration of $3.5\%$.
$\frac{2c \, + \, 15}{500} = \frac{3.5 \text{ g of Sugar}}{100 \text{ g of Pamela's}}$
Solving for $c$ we get:
$c = 1.25$ g of sugar $= 1.25\%$ concentration
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
SAT Main Menu >>
