Difficulty Level – 3: Medium / Difficult
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Evaluate: $\, \dfrac{i^2+1}{i} \div \dfrac{i-1}{i^2-1}$
$− 2$ | |
$− 1$ | |
$0$ | |
$1$ | |
$2$ |
Question 1 Explanation:
The correct answer is (C). This initially looks very complicated; however, recall that $i$ is equal to the square root of −1, so $i^2$ is equal to −1. Evaluating the numerator of the expression on the left gives us 0. Because we are dividing the first expression by the second, and 0 divided by anything is 0, the entire expression evaluates to 0.
$\dfrac{i^2 + 1}{i} ÷ \dfrac{i - 1}{i^2 - 1}$
$\dfrac{i^2 + 1}{i} ⋅ \dfrac{i^2 - 1}{i - 1}$
$\dfrac{(-1) + 1}{i} ⋅ \dfrac{(-1) - 1}{i - 1}$
$\dfrac{0}{i} ⋅ \dfrac{-2}{i - 1}$
$\dfrac{(0)(-2)}{(i)(i - 1)}$
$\dfrac{0}{(i)(i - 1)}$
$0$
$\dfrac{i^2 + 1}{i} ÷ \dfrac{i - 1}{i^2 - 1}$
$\dfrac{i^2 + 1}{i} ⋅ \dfrac{i^2 - 1}{i - 1}$
$\dfrac{(-1) + 1}{i} ⋅ \dfrac{(-1) - 1}{i - 1}$
$\dfrac{0}{i} ⋅ \dfrac{-2}{i - 1}$
$\dfrac{(0)(-2)}{(i)(i - 1)}$
$\dfrac{0}{(i)(i - 1)}$
$0$
Question 2 |
What is the sum of the $x$ and $y$ coordinates of the midpoint between the points $(−2, 9)$ and $(10, −4)$?
$3.5$ | |
$5$ | |
$6.5$ | |
$7.5$ | |
$8$ |
Question 2 Explanation:
The correct answer is (C). Recall midpoint formula is the average of the $x$ values and the average of the $y$ values in $(x, y)$ coordinate form.
First find the $x$ coordinate midpoint:
$(10 + (−2)) ÷ 2$
$= 4$
Then find the y coordinate midpoint:
$(9 + (−4)) ÷ 2$
$= 2.5$
Add them together to get the sum:
$4 + 2.5 = 6.5$
First find the $x$ coordinate midpoint:
$(10 + (−2)) ÷ 2$
$= 4$
Then find the y coordinate midpoint:
$(9 + (−4)) ÷ 2$
$= 2.5$
Add them together to get the sum:
$4 + 2.5 = 6.5$
Question 3 |
A group of 6 students are going to have a vote to determine who should be President, Vice President, Secretary, and Treasurer with only 1 person per job. How many different groups can be formed from the 6 students?
$30$ | |
$45$ | |
$90$ | |
$180$ | |
$360$ |
Question 3 Explanation:
The correct answer is (E). This is a permutation since the four roles are different and, thus, the order in which they are selected matters. In approaching this problem, consider the number of options the students have for each role. As a role is taken up, there is 1 less student to fill the next role. For President there are 6 options, for Vice President 5 options, for Secretary 4 options, and for Treasurer 3 options. Multiply each of these to find 360 different groups:
$6 \ast 5 \ast 4 \ast 3 = 360$
Alternatively, if your calculator has a permutation function you can enter:
$_6P_4$
This will give the same answer, $360$.
$6 \ast 5 \ast 4 \ast 3 = 360$
Alternatively, if your calculator has a permutation function you can enter:
$_6P_4$
This will give the same answer, $360$.
Question 4 |
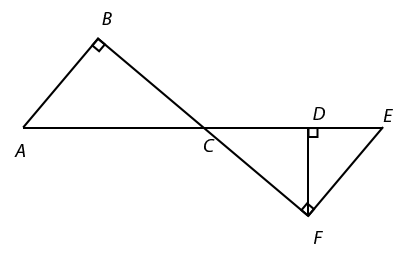
In the figure above, A, C, D, and E are collinear; B, C, and F are collinear; and the angles at B, D, and F are right angles, as marked. Which of the following statements is NOT justifiable from the given information?
$\overline{AB}$ is parallel to $\overline{EF}$ | |
$\overline{BC}$ is congruent to $\overline{CF}$ | |
$\overline{EF}$ is perpendicular to $\overline{BF}$ | |
$\angle BCA$ is congruent to $\angle DCF$ | |
$\Delta BAC$ is parallel to $\Delta DFC$ |
Question 4 Explanation:
The correct answer is (B). Solve this by process of elimination.
(A): True: $\overline{BC}$ and $\overline{EF}$ are both perpendicular to $\overline{BF}$.
(C): True: $\angle BFE$ is a right angle, so the two segments are perpendicular.
(D): True: $\angle BCA$ and $\angle DCF$ are vertical angles, so they must be congruent.
(E): True: $\angle ABC ≅ \angle CDF$ (they are both right angles) and $\angle BCA ≅ \angle DCF$. $\Delta BAC$ ~ $\Delta DFC$ by the "$AA$ postulate".
(B): False: Although we know that $\Delta BAC$ ~ $\Delta DFC$, we cannot prove that they are congruent; their corresponding sides may not be congruent.
(A): True: $\overline{BC}$ and $\overline{EF}$ are both perpendicular to $\overline{BF}$.
(C): True: $\angle BFE$ is a right angle, so the two segments are perpendicular.
(D): True: $\angle BCA$ and $\angle DCF$ are vertical angles, so they must be congruent.
(E): True: $\angle ABC ≅ \angle CDF$ (they are both right angles) and $\angle BCA ≅ \angle DCF$. $\Delta BAC$ ~ $\Delta DFC$ by the "$AA$ postulate".
(B): False: Although we know that $\Delta BAC$ ~ $\Delta DFC$, we cannot prove that they are congruent; their corresponding sides may not be congruent.
Question 5 |
If (3.1358)(10$^x$) = 0.0000031358 what is the value of $x$?
$− 7$ | |
$− 6$ | |
$− 5$ | |
$6$ | |
$7$ |
Question 5 Explanation:
The correct answer is (B). The easiest way to solve this problem is to count how many places the decimal moves from the number on the left to the number on the right. Our decimal moves 6 places to the left, so $x$ = −6.
Question 6 |
A triangle is composed of angles represented as:
$3x + 10$, $−2x + 40$, and $x + 40$
What is the value of $x$?
$45$ | |
$50$ | |
$55$ | |
$60$ | |
$65$ |
Question 6 Explanation:
The correct answer is (A). Recall that the angles of a triangle sum to 180 degrees:
$3x + 10 + −2x + 40 + x $ $ + \, 40 $ $ = 180$
$2x + 90 = 180$
$2x = 90$
$x = 45$
$3x + 10 + −2x + 40 + x $ $ + \, 40 $ $ = 180$
$2x + 90 = 180$
$2x = 90$
$x = 45$
Question 7 |
$\dfrac{−2x+3y(2x-4)}{4x−2y} = \; ?$
$4x −\dfrac{6xy}{x−y}$ | |
$\dfrac{2x+6xy−8y}{2x−y}$ | |
$\dfrac{6xy−x+y}{2x}$ | |
$\dfrac{8x+4xy}{3xy}$ | |
$\dfrac{x−3xy+6y}{y−2x}$ |
Question 7 Explanation:
The correct answer is (E). Simplify as shown here:
$\dfrac{-2x + 3y(2x - 4)}{4x - 2y}$
$\dfrac{-2x + (3y)(2x) + (3y)(-4)}{4x - 2y}$
$\dfrac{-2x + 6xy - 12y}{4x - 2y}$
$\dfrac{-2(x - 3xy + 6y)}{-2(-2x + y)}$
$\dfrac{x - 3xy + 6y}{-2x + y}$
$\dfrac{x - 3xy + 6y}{y - 2x}$
$\dfrac{-2x + 3y(2x - 4)}{4x - 2y}$
$\dfrac{-2x + (3y)(2x) + (3y)(-4)}{4x - 2y}$
$\dfrac{-2x + 6xy - 12y}{4x - 2y}$
$\dfrac{-2(x - 3xy + 6y)}{-2(-2x + y)}$
$\dfrac{x - 3xy + 6y}{-2x + y}$
$\dfrac{x - 3xy + 6y}{y - 2x}$
Question 8 |
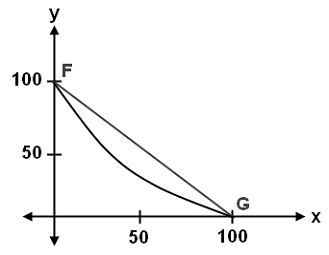
The curve $y = 0.01x^2 - 3x + 150$ for $0 ≤ x ≤ 100$ and the line segment from $F(0,100)$ to $G(100,0)$ are shown in the standard $(x, y)$ coordinate plane.
What is the $x$-coordinate for the point on the curve with a $y$-coordinate of $50$? (Round to the nearest whole number.)
$29$ | |
$31$ | |
$38$ | |
$47$ | |
$35$ |
Question 8 Explanation:
The correct answer is (C). We are asked to find the $x$-coordinate corresponding to a $y$-coordinate of $50$.
Substitute $y = 50$ into the equation for the curve and solve for $x$:
$50 = 0.01x^2 - 3x + 150$
$0 = 0.01x^2 - 3x + 100$
Here we can either use the quadratic formula or use the quadratic solver on our calculator (if it has one):
$x = \dfrac{-b ± \sqrt{b^2 - 4ac}}{2a}$
$x = $ $ \dfrac{-(-3) ± \sqrt{(-3)^2 - 4(0.01)(100)}}{2(0.01)}$
$x = \dfrac{3 ± \sqrt{5}}{0.02}$
$x ≈ 38.19$ or $x ≈ 261.80$ (outside the $0 ≤ x ≤ 100$ domain)
Substitute $y = 50$ into the equation for the curve and solve for $x$:
$50 = 0.01x^2 - 3x + 150$
$0 = 0.01x^2 - 3x + 100$
Here we can either use the quadratic formula or use the quadratic solver on our calculator (if it has one):
$x = \dfrac{-b ± \sqrt{b^2 - 4ac}}{2a}$
$x = $ $ \dfrac{-(-3) ± \sqrt{(-3)^2 - 4(0.01)(100)}}{2(0.01)}$
$x = \dfrac{3 ± \sqrt{5}}{0.02}$
$x ≈ 38.19$ or $x ≈ 261.80$ (outside the $0 ≤ x ≤ 100$ domain)
Question 9 |
For $\Delta ABC$ below, what is $\cos(C)$?
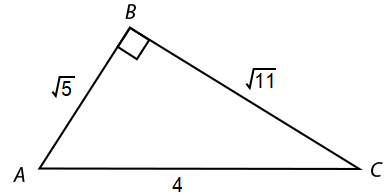
$\dfrac{4\sqrt{5}}{5}$ | |
$\dfrac{\sqrt{5}}{4}$ | |
$\dfrac{\sqrt{11}}{4}$ | |
$\dfrac{\sqrt{55}}{5}$ | |
$\dfrac{\sqrt{55}}{11}$ |
Question 9 Explanation:
The correct answer is (C).
Label the sides relative to $\angle C$:
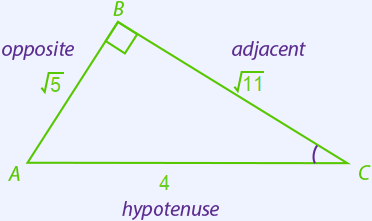
$\cos(C) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{\sqrt{11}}{4}$
Label the sides relative to $\angle C$:

$\cos(C) = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{\sqrt{11}}{4}$
Question 10 |
On the Cartesian plane, a circle has its center at $(0,0)$. If the point $(5,-5)$ lies on the circle, what is the diameter of the circle?
$10$ | |
$7 \sqrt{2}$ | |
$50$ | |
$14$ | |
$10 \sqrt{2}$ |
Question 10 Explanation:
The correct answer is (E). The radius of a circle is defined as the distance from its center to a point on the circle.
Using the distance formula we can find the radius of our circle:
$r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
$r = \sqrt{(5 - 0)^2 + (-5 - 0)^2}$
$r = \sqrt{50}$
$r = 5\sqrt{2}$
The diameter is twice its radius:
$D = 2r$
$D = 2(5\sqrt{2})$
$D = 10\sqrt{2}$
Using the distance formula we can find the radius of our circle:
$r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$
$r = \sqrt{(5 - 0)^2 + (-5 - 0)^2}$
$r = \sqrt{50}$
$r = 5\sqrt{2}$
The diameter is twice its radius:
$D = 2r$
$D = 2(5\sqrt{2})$
$D = 10\sqrt{2}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 7 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
