Difficulty Level – 4: Difficult
Directions: Solve each problem and then click on the correct answer. You are permitted to use a calculator on this test.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Each term in a sequence of numbers is created by halving the previous number in the sequence, multiplying it by 3 and subtracting 5. If the 3rd number in this sequence is 41.5, what is the first number in the sequence?
$12$ | |
$18$ | |
$24$ | |
$31$ | |
$35$ |
Question 1 Explanation:
The correct answer is (C). Use the final number and the steps listed to get there to work backward to find the first number. Set up an equation to represent the situation:
$a_n=\dfrac{1}{2}a_{n−1} *3-5$
$a_3=41.5=\dfrac{1}{2}a_2 *3-5$
$a_2=31$
$a_2=31=\dfrac{1}{2}a_1 *3-5$
$a_1=24$
Alternate approach:
To get from the “current number” to the “next number”, we follow these steps:
(1) take half of the number
(2) multiply by 3
(3) subtract 5
That means to get from the “current number” to the “previous number” we would need to go in the reverse order and “undo” each of the steps (use the inverse function):
(1) add 5
(2) divide by 3
(3) double the number
To get from the 3rd number, 41.5, to the 2nd number:
(1) add 5: 41.5 + 5 = 46.5
(2) divide by 3: 46.5 ÷ 3 = 15.5
(3) double the number: 15.5 ∗ 2 = 31
To get from the 2nd number, 31, to the 1st number:
(1) add 5: 31 + 5 = 36
(2) divide by 3: 36 ÷ 3 = 12
(3) double the number: 12 ∗ 2 = 24
$a_n=\dfrac{1}{2}a_{n−1} *3-5$
$a_3=41.5=\dfrac{1}{2}a_2 *3-5$
$a_2=31$
$a_2=31=\dfrac{1}{2}a_1 *3-5$
$a_1=24$
Alternate approach:
To get from the “current number” to the “next number”, we follow these steps:
(1) take half of the number
(2) multiply by 3
(3) subtract 5
That means to get from the “current number” to the “previous number” we would need to go in the reverse order and “undo” each of the steps (use the inverse function):
(1) add 5
(2) divide by 3
(3) double the number
To get from the 3rd number, 41.5, to the 2nd number:
(1) add 5: 41.5 + 5 = 46.5
(2) divide by 3: 46.5 ÷ 3 = 15.5
(3) double the number: 15.5 ∗ 2 = 31
To get from the 2nd number, 31, to the 1st number:
(1) add 5: 31 + 5 = 36
(2) divide by 3: 36 ÷ 3 = 12
(3) double the number: 12 ∗ 2 = 24
Question 2 |

A rectangle is inscribed inside of a circle in the figure above. What is the length of twice the circumference?
$5π$ $\text{in}$ | |
$10π$ $\text{in}$ | |
$15π$ $\text{in}$ | |
$20π$ $\text{in}$ | |
$30π$ $\text{in}$ |
Question 2 Explanation:
The correct answer is (B). Here we may use Pythagoras’ Theorem to find the diagonal of the rectangle, which is also equal to the circle’s diameter:
$3^2 + 4^2 = 5^2 = 25 = D^2$
The diameter, $D = 5$
The formula for the circumference of a circle is:
$C = 2πr = πd → C = 5 π$
But, we are asked for twice the circumference, so we must complete one more step:
$2 * 5π = 10π \text{ in}$
$3^2 + 4^2 = 5^2 = 25 = D^2$
The diameter, $D = 5$
The formula for the circumference of a circle is:
$C = 2πr = πd → C = 5 π$
But, we are asked for twice the circumference, so we must complete one more step:
$2 * 5π = 10π \text{ in}$
Question 3 |
If 68% of a number is 102, what is 250% of the same number?
$186$ | |
$246$ | |
$255$ | |
$287$ | |
$375$ |
Question 3 Explanation:
The correct answer is (E). We will use the definition of percentages to answer this question. An unknown number, when multiplied by 68% is 102:
$0.68*x=102$
$x=\dfrac{102}{.68}=150$
To find 250% of this number:
$150*2.5=375$
$0.68*x=102$
$x=\dfrac{102}{.68}=150$
To find 250% of this number:
$150*2.5=375$
Question 4 |
In the figure provided below, all line segments meet at right angles. What is the area of the figure?
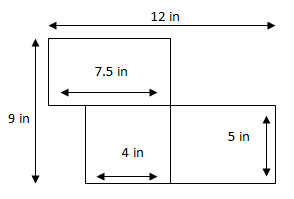
$62.5$ $\text{in}$$^2$ | |
$65$ $\text{in}$$^2$ | |
$70$ $\text{in}$$^2$ | |
$72.5$ $\text{in}$$^2$ | |
$75$ $\text{in}$$^2$ |
Question 4 Explanation:
The correct answer is (D). There are two methods for calculating the area of the figure (the 3 adjacent boxes): one method is to calculate the area of the largest figure, outlined by the 12 inch line on the top and the 9 inch line on the side, then subtract from this total area the areas of the 2 smaller boxes that are not part of the figure; another method is to individually calculate the area of each box and combine them. The first method seems less involved so we will choose that:
Area of large outline:
$12 * 9 = 108$
The area of the bottom left rectangle:
$5 * 3.5 = 17.5$
Area of the top right rectangle:
$4.5 * 4 = 18$
Sum these 2 areas and subtract from the larger area:
$108 − 35.5 = 72.5$
It may not be obvious where the numbers for these calculations came from, but upon inspecting the figure, we can find out the unknown measurements of each side length: subtracting the known height of 5 inches from the total height of 9 inches gives us the 4 inch height for the top right portion. In similar fashion, subtracting 7.5 inches from the total length of 12 inches gives us 4.5 inches for the length of the top right portion. The bottom left portion’s length can be found by subtracting 4 inches from 7.5 inches to find 3.5 inches. The bottom left portion's height is 5 inches (the same as the two rectangles to its right). When working through this problem, and problems like it, it is best to label each found measurement to avoid having to remember.
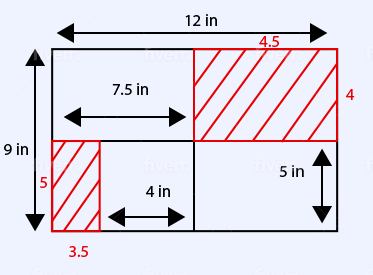
Area of large outline:
$12 * 9 = 108$
The area of the bottom left rectangle:
$5 * 3.5 = 17.5$
Area of the top right rectangle:
$4.5 * 4 = 18$
Sum these 2 areas and subtract from the larger area:
$108 − 35.5 = 72.5$
It may not be obvious where the numbers for these calculations came from, but upon inspecting the figure, we can find out the unknown measurements of each side length: subtracting the known height of 5 inches from the total height of 9 inches gives us the 4 inch height for the top right portion. In similar fashion, subtracting 7.5 inches from the total length of 12 inches gives us 4.5 inches for the length of the top right portion. The bottom left portion’s length can be found by subtracting 4 inches from 7.5 inches to find 3.5 inches. The bottom left portion's height is 5 inches (the same as the two rectangles to its right). When working through this problem, and problems like it, it is best to label each found measurement to avoid having to remember.

Question 5 |
What is the expression $−3(4 + i) − (i^2 + 3i)$, where $i$ is imaginary, equivalent to?
$− 12 − 7i$ | |
$− 11 − 6i$ | |
$− 11$ | |
$− 13 − 6i$ | |
$− 13 − 7i$ |
Question 5 Explanation:
The correct answer is (B). To solve this problem, we will follow the order of operations until we have simplified the expression as much as we can. It will be important to recall that $i^2 = −1.$
Using the distributive property, we find:
$−12 − 3i − i^2 − 3i$
$−12 − 3i −(−1) − 3i$
$−11 − 6i$
Using the distributive property, we find:
$−12 − 3i − i^2 − 3i$
$−12 − 3i −(−1) − 3i$
$−11 − 6i$
Question 6 |
What is the 60th term in the following arithmetic sequence?
−4, 1, 6, 11 . . .
$289$ | |
$290$ | |
$291$ | |
$292$ | |
$293$ |
Question 6 Explanation:
The correct answer is (C). If we recall the formula for finding the nth term of an arithmetic sequence, this problem is quite easy; however, we do not always easily recall formulas. It is also unlikely that we are expected to continue counting out the entire sequence to solve for the 60th term, so it is likely that there is some counting trick at work here. We know that the first term is −4, and we know that the sequence is generated by adding 5 to each previous term. This means that to the first term, we must add 1 less than 60 times 5 to find what the 60th term will be:
$−4 + 59 * 5 = 291$
Recalling the formula for calculating the $n^{th}$ term in a sequence:
$a_n = a_1 + (n − 1)d$ where $a_n$ is the $n^{th}$ term, $a_1$ is the 1st term, $n$ is the term we’re looking for, and $d$ is the difference between each consecutive term we find:
$a_n = −4 + (60 − 1)5 = 291$
$−4 + 59 * 5 = 291$
Recalling the formula for calculating the $n^{th}$ term in a sequence:
$a_n = a_1 + (n − 1)d$ where $a_n$ is the $n^{th}$ term, $a_1$ is the 1st term, $n$ is the term we’re looking for, and $d$ is the difference between each consecutive term we find:
$a_n = −4 + (60 − 1)5 = 291$
Question 7 |
If the domain of $f(x) = (x − 2)^2 + 2$ is all real numbers from −3 to 4, what is the range of $f(x)$?
$− 3 \le ƒ(x) \le 4$ | |
$0 \le ƒ(x) \le 27$ | |
$2 \le ƒ(x) \le 27$ | |
$3 \le ƒ(x) \le 27$ | |
$2 \le ƒ(x) \le16$ |
Question 7 Explanation:
The correct answer is (C). Recall that the range of a function is the y-values for which the function is defined. We should also recognize this function as a parabola with vertex at (2, 2) and remember that the vertex of a parabola is either its maximum or minimum value, depending on its orientation. In this case, because this parabola is positively oriented, the vertex will be the minimum value, so we know that our range must begin at 2. To find the maximum value of the range, we will plug in the end points of the listed domain:
$f(−3) = (−3 − 2)^2 + 2 = 27$
and
$f(4) = (4 − 2)^2 + 2 = 6$
We can see that our range will extend from 2 to 27, so answer choice (C) is correct.
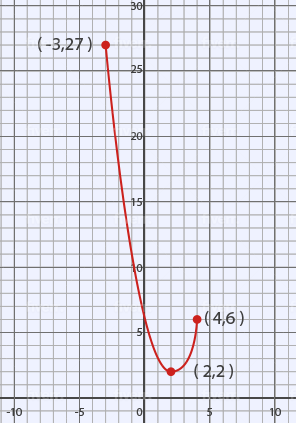
$f(−3) = (−3 − 2)^2 + 2 = 27$
and
$f(4) = (4 − 2)^2 + 2 = 6$
We can see that our range will extend from 2 to 27, so answer choice (C) is correct.

Question 8 |
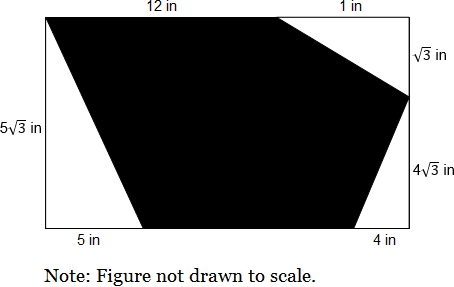
A 5-sided figure (shown in black) is created by taking a rectangle and removing three right triangles. What is the perimeter, in inches, of the 5-sided figure?
$12 + 2\sqrt{2} + 9\sqrt{3}$ | |
$17 + \sqrt{2} + 4\sqrt{3}$ | |
$19 + \sqrt{2} + 5\sqrt{3}$ | |
$23 + 2\sqrt{2} + 9\sqrt{3}$ | |
$36$ |
Question 8 Explanation:
The correct answer is (E). Because we are told that each of the triangles are right triangles, we could use Pythagorean’s Theorem to find the length of each triangle's hypotenuse, then sum these with the lengths of the shaded figure’s other two sides.
In 30°, 60°, 90° triangles, the relationship between the side lengths is $x$, $x \sqrt{3}$, $2x$, respectively. We can then see that for the bottom left triangle, the hypotenuse will be 10, and for the bottom right triangle, 8. We can also see that the top right triangle’s hypotenuse will be 2. We know from the top length that the total length of the rectangle is 13, so the bottom side length of the shaded figure must be:
$13 − (4 + 5) = 4$
Now we can sum these all together to find the total perimeter of the shaded region:
$2 + 8 + 4 + 10 + 12 = 36$
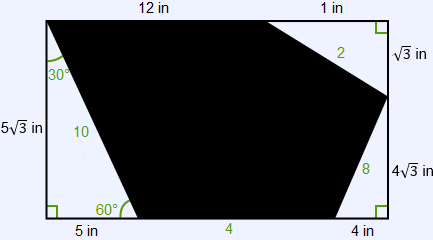
In 30°, 60°, 90° triangles, the relationship between the side lengths is $x$, $x \sqrt{3}$, $2x$, respectively. We can then see that for the bottom left triangle, the hypotenuse will be 10, and for the bottom right triangle, 8. We can also see that the top right triangle’s hypotenuse will be 2. We know from the top length that the total length of the rectangle is 13, so the bottom side length of the shaded figure must be:
$13 − (4 + 5) = 4$
Now we can sum these all together to find the total perimeter of the shaded region:
$2 + 8 + 4 + 10 + 12 = 36$

Question 9 |
A circle is drawn in the Cartesian plane. It is drawn tangent to the y-axis at −7 and tangent to the x-axis at 7. What is the equation of the circle?
$(x − 7)^2 + (y + 7)^2 = 49$ | |
$x^2 + y^2 = 49$ | |
$(x + 7)^2 + (y + 7)^2 = 49$ | |
$(x + 7)^2 + (y − 7)^2 = 49$ | |
$x^2 + y^2 = 7$ |
Question 9 Explanation:
The correct answer is (A). Recall that the equation of a circle centered at $(h, k)$ is $(x − h)^2 + (y − k)² = r^2$ where $r$ is the radius.
We are given a circle that touches the x-axis at the point $(7, 0)$ and the y-axis at $(0, −7)$. Using this information, we can conclude that our circle is centered at $(7, −7)$. Using this information we can rewrite the equation of a circle to:
$(x – 7)^2 + (y + 7)^2 = 49$
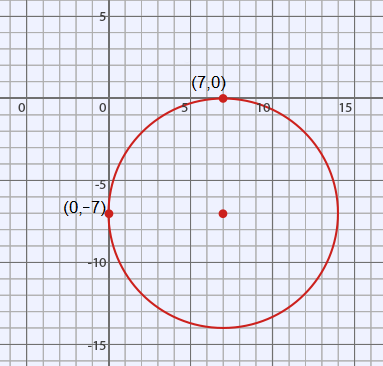
We are given a circle that touches the x-axis at the point $(7, 0)$ and the y-axis at $(0, −7)$. Using this information, we can conclude that our circle is centered at $(7, −7)$. Using this information we can rewrite the equation of a circle to:
$(x – 7)^2 + (y + 7)^2 = 49$

Question 10 |
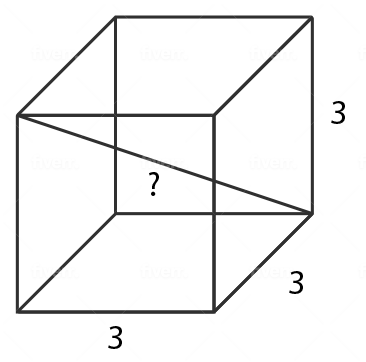
The side length of a cube is 3 units, what is the length of the cube’s diagonal?
$12$ | |
$12\sqrt{2}$ | |
$27$ | |
$27\sqrt{2}$ | |
$3\sqrt{3}$ |
Question 10 Explanation:
The correct answer is (E). The formula for the diagonal of a rectangular solid with length $(l)$, width $(w)$, and height $(h)$ is:
$D = \sqrt{l^2 + w^2 + h^2}$
Since a cube has side length $s = l= w= h$, we can derive a formula for the side of a cube as follows:
$D = \sqrt{s^2 + s^2 + s^2} = \sqrt{3s^2} $ $ = \sqrt{3}\sqrt{s^2}$
$D = s\sqrt{3}$
Since $s = 3$:
$D = 3\sqrt{3}$
$D = \sqrt{l^2 + w^2 + h^2}$
Since a cube has side length $s = l= w= h$, we can derive a formula for the side of a cube as follows:
$D = \sqrt{s^2 + s^2 + s^2} = \sqrt{3s^2} $ $ = \sqrt{3}\sqrt{s^2}$
$D = s\sqrt{3}$
Since $s = 3$:
$D = 3\sqrt{3}$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
ACT Math Practice Test 9 >>
More Practice Tests:
ACT Math – Main Menu >>
ACT Science Practice >>
ACT English Practice >>
ACT Reading Practice >>
