This is our free AP Calculus AB unit test on limits. These questions cover basic limits, limit properties, limits of infinity, limits at infinity, and L’Hopital’s rule. Understanding these properties of limits is very important when analyzing the behavior of functions and evaluating integrals. Additionally, understanding the concept of continuity is essential for various calculus operations.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
$\lim\limits_{x\to -\infty} e^x + 4$
$\text{DNE}$ | |
$4$ | |
$∞$ | |
$-4$ |
Question 1 Explanation:
The correct answer is (B). Recall that limits can “distribute” across addition, such that:
$\lim\limits_{x\to -\infty} e^x + 4 =$ $\lim\limits_{x\to -\infty} e^x + \lim\limits_{x\to -\infty} 4$
It may be beneficial to visualize the graph of the function $e^x$ when evaluating the first limit in the sum, as the function approaches $0$ as $x$ approaches $∞$. Also recall that the limit of any constant is just itself. Therefore:
$\lim\limits_{x\to -\infty} e^x + \lim\limits_{x\to -\infty} 4 =$ $0 + 4 = 4$
$\lim\limits_{x\to -\infty} e^x + 4 =$ $\lim\limits_{x\to -\infty} e^x + \lim\limits_{x\to -\infty} 4$
It may be beneficial to visualize the graph of the function $e^x$ when evaluating the first limit in the sum, as the function approaches $0$ as $x$ approaches $∞$. Also recall that the limit of any constant is just itself. Therefore:
$\lim\limits_{x\to -\infty} e^x + \lim\limits_{x\to -\infty} 4 =$ $0 + 4 = 4$
Question 2 |
$\lim\limits_{x\to 1} \dfrac{x − 1}{\ln(x)}$
$0$ | |
$\text{DNE}$ | |
$1$ | |
$−1$ |
Question 2 Explanation:
The correct answer is (C). Evaluating the limit directly results in $\frac{1 \, − \, 1}{\ln (1)} = \frac{0}{0}$.
Since this is an indeterminate form, we must apply L’Hôpital’s rule. Setting $f(x) = x − 1$ and $g(x) = \ln (x)$ and applying L’Hôpital’s rule, we get:
$\dfrac{f'(x)}{g'(x)} = \dfrac{1}{\left(\frac{1}{x}\right)} = x$
Evaluating the limit as $\frac{f'(x)}{g'(x)}$ approaches 1, we see that: $\lim\limits_{x\to 1} \frac{x − 1}{\ln(x)} = 1$
Since this is an indeterminate form, we must apply L’Hôpital’s rule. Setting $f(x) = x − 1$ and $g(x) = \ln (x)$ and applying L’Hôpital’s rule, we get:
$\dfrac{f'(x)}{g'(x)} = \dfrac{1}{\left(\frac{1}{x}\right)} = x$
Evaluating the limit as $\frac{f'(x)}{g'(x)}$ approaches 1, we see that: $\lim\limits_{x\to 1} \frac{x − 1}{\ln(x)} = 1$
Question 3 |
$\lim\limits_{x\to 0} \dfrac{\cos(2x)}{x}$
$0$ | |
$\text{DNE}$ | |
$2$ | |
$1$ |
Question 3 Explanation:
The correct answer is (B). Notice that the limit evaluates to $\frac{1}{0}$ by direct substitution, which is not an indeterminate form. This implies that the limit is undefined, and therefore does not exist.
Question 4 |
$\lim\limits_{x\to 0} \dfrac{x^2}{|x|}$
$1$ | |
$\text{DNE}$ | |
$2$ | |
$0$ |
Question 4 Explanation:
The correct answer is (D). Notice that the limit evaluates to $\frac{0}{0}$ by direct substitution, which is one of the indeterminate forms that justifies the use of L’Hôpital’s rule. Therefore, after taking the derivative of the numerator and denominator:
$\lim\limits_{x\to 0} \dfrac{x^2}{|x|} = \lim\limits_{x\to 0} \dfrac{2x}{±1} = \dfrac{2(0)}{±1}$ $= 0$
Do not let the absolute value sign confuse the derivation of the denominator, as the derivative of the absolute value of $x$ is a piece-wise defined function of the form below.
$|x|' = \begin{cases} -1, & \text{x < 0} \\ ~~~1, & \text{x > 0} \end{cases}$
$\lim\limits_{x\to 0} \dfrac{x^2}{|x|} = \lim\limits_{x\to 0} \dfrac{2x}{±1} = \dfrac{2(0)}{±1}$ $= 0$
Do not let the absolute value sign confuse the derivation of the denominator, as the derivative of the absolute value of $x$ is a piece-wise defined function of the form below.
$|x|' = \begin{cases} -1, & \text{x < 0} \\ ~~~1, & \text{x > 0} \end{cases}$
Question 5 |
For the function below, identify the following limit:
$\lim\limits_{x\to 3} f(x)$
$f(x) =
\begin{cases}
–x^2 + 7, & x ≤ 3 \\[1ex]
~~~~x − 5, & {x ≥ 3}
\end{cases}$
$−2$ | |
$\text{DNE}$ | |
$2$ | |
$0$ |
Question 5 Explanation:
The correct answer is (A). Even though the function $f(x)$ is piece-wise defined, it is still a continuous because the limit as $x$ approaches $3$ exists.
We evaluate the given limit by identifying the limit value as $x$ approaches $3$ from the positive and negative side of the piece-wise defined function.
Note that: $\lim\limits_{x\to 3^−}–x^2 + 7 = −2~$ and $\lim\limits_{x\to 3^+} x − 5 = −2$
Therefore, the limit exists, as the function approaches $−2$ from both the positive and negative sides of the function.
We evaluate the given limit by identifying the limit value as $x$ approaches $3$ from the positive and negative side of the piece-wise defined function.
Note that: $\lim\limits_{x\to 3^−}–x^2 + 7 = −2~$ and $\lim\limits_{x\to 3^+} x − 5 = −2$
Therefore, the limit exists, as the function approaches $−2$ from both the positive and negative sides of the function.
Question 6 |
Identify which of the following functions is increasing at a faster rate on the given domain.
$f(x) = x^2$, $x ≥ 1$
$g(x) = x$, $x ≥ 1$
$g(x) = x$ | |
$f(x) = x^2$ | |
$\text{Insufficient information}$ | |
$\text{Both functions increase}$ $\text{at the same rate}$ |
Question 6 Explanation:
The correct answer is (B). It is important to recognize that identifying rates of change is an application of the derivative. We can identify which function is increasing at a faster rate by evaluating a ratio:
$\dfrac{f(x)}{g(x)} = \dfrac{x^2}{x}$
It is also important to recognize that L’Hôpital’s rule is simply a method for identifying rates of change. Thus, we can take the derivative of each function and also write those as a ratio:
$\dfrac{f'(x)}{g'(x)} = \dfrac{2x}{1}$
Note that for $x ≥ 1$, the given domain, that $2x > 1$. Therefore, the rate of change of $f(x)$ is greater than $g(x)$ on the domain. Also note that $2x$ is positive for all $x ≥ 1$, which implies that $f(x)$ is increasing on this domain. Therefore, $f(x)$ is increasing at a faster rate than $g(x)$.
$\dfrac{f(x)}{g(x)} = \dfrac{x^2}{x}$
It is also important to recognize that L’Hôpital’s rule is simply a method for identifying rates of change. Thus, we can take the derivative of each function and also write those as a ratio:
$\dfrac{f'(x)}{g'(x)} = \dfrac{2x}{1}$
Note that for $x ≥ 1$, the given domain, that $2x > 1$. Therefore, the rate of change of $f(x)$ is greater than $g(x)$ on the domain. Also note that $2x$ is positive for all $x ≥ 1$, which implies that $f(x)$ is increasing on this domain. Therefore, $f(x)$ is increasing at a faster rate than $g(x)$.
Question 7 |
Identify which of the following functions is increasing at a faster rate on the given domain.
$f(x) = x^3 − 3x$, $2 ≤ x < ∞$
$g(x) = x^3$, $2 ≤ x < ∞$
$f(x) = x^3 − 3x$ | |
$g(x) = x^3$ | |
$\text{Insufficient information}$
| |
$\text{Both functions increase}$ $\text{at the same rate}$ |
Question 7 Explanation:
The correct answer is (B). It is important to recognize that identifying rates of change is an application of the derivative. We can identify which function is increasing at a faster rate by evaluating a ratio:
$\dfrac{f(x)}{g(x)} = \dfrac{x^3 − 3x}{x^3}$
It is also important to recognize that L’Hôpital’s rule is simply a method for identifying rates of change. Thus, we can take the derivative of each function and also write those as a ratio:
$\dfrac{f'(x)}{g'(x)} = \dfrac{3x^2 − 3}{3x^2}$
Note that for $x ≥ 2$, the given domain, $f'(x)$ and $g'(x)$ are positive, which implies that $f(x)$ and $g(x)$ are increasing on this domain. Note that $3x^2 − 3 < 3x^2$ for all $x ≥ 2$. Therefore, $g(x)$ is increasing at a faster rate than $f(x)$.
$\dfrac{f(x)}{g(x)} = \dfrac{x^3 − 3x}{x^3}$
It is also important to recognize that L’Hôpital’s rule is simply a method for identifying rates of change. Thus, we can take the derivative of each function and also write those as a ratio:
$\dfrac{f'(x)}{g'(x)} = \dfrac{3x^2 − 3}{3x^2}$
Note that for $x ≥ 2$, the given domain, $f'(x)$ and $g'(x)$ are positive, which implies that $f(x)$ and $g(x)$ are increasing on this domain. Note that $3x^2 − 3 < 3x^2$ for all $x ≥ 2$. Therefore, $g(x)$ is increasing at a faster rate than $f(x)$.
Question 8 |
$\lim\limits_{x\to \infty} \dfrac{2x^2}{\ln(\sqrt{x})}$
$0$ | |
$2$ | |
$4$ | |
$\text{DNE}$ |
Question 8 Explanation:
The correct answer is (D). Notice that the limit evaluates to $\frac{∞}{∞}$ by direct substitution, which is one of the indeterminate forms that justifies the use of L’Hôpital’s rule. It is important to be careful with your derivation and to remember chain rule when identifying the derivative of $\ln(\sqrt{x})$.
Note that:
$\dfrac{d}{dx}(\ln(\sqrt{x}))$ $= \dfrac{1}{\sqrt{x}} \cdot (\dfrac{1}{2}x^{–\frac{1}{2}})$ $= \dfrac{1}{2} \cdot \dfrac{1}{\sqrt{x}} \cdot \dfrac{1}{\sqrt{x}}$ $= \dfrac{1}{2x}$
Therefore, by L’Hôpital’s rule:
$\lim\limits_{x\to \infty} \dfrac{2x^2}{\ln(\sqrt{x})}$ $= \lim\limits_{x\to \infty} \dfrac{4x}{\frac{1}{2x}}$ $= \lim\limits_{x\to -\infty} 4x \cdot 2x$ $+ \lim\limits_{x\to \infty} 8x^2$
Notice then that this limit evaluates to $∞$, which implies that the limit does not exist.
Note that:
$\dfrac{d}{dx}(\ln(\sqrt{x}))$ $= \dfrac{1}{\sqrt{x}} \cdot (\dfrac{1}{2}x^{–\frac{1}{2}})$ $= \dfrac{1}{2} \cdot \dfrac{1}{\sqrt{x}} \cdot \dfrac{1}{\sqrt{x}}$ $= \dfrac{1}{2x}$
Therefore, by L’Hôpital’s rule:
$\lim\limits_{x\to \infty} \dfrac{2x^2}{\ln(\sqrt{x})}$ $= \lim\limits_{x\to \infty} \dfrac{4x}{\frac{1}{2x}}$ $= \lim\limits_{x\to -\infty} 4x \cdot 2x$ $+ \lim\limits_{x\to \infty} 8x^2$
Notice then that this limit evaluates to $∞$, which implies that the limit does not exist.
Question 9 |
Identify the following limit using the graph below. Note that the graphs $f(x)$ and $g(x)$ are labeled by $f$ and $g$ respectively.
 $\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$
$\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$
 $\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$
$\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$
$−\dfrac{1}{2}$ | |
$2$ | |
$−2$ | |
$−\dfrac{2}{3}$ |
Question 9 Explanation:
The correct answer is (C). Recall that limits have the division property such that:
$\lim\limits_{x\to a} \dfrac{f(x)}{g(x)}$ $= \dfrac{\lim\limits_{x\to a}f(x)}{\lim\limits_{x\to a}f(x)}$
Therefore:
$\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$ $= \dfrac{\lim\limits_{x\to 2}f(x)}{\lim\limits_{x\to 2}f(x)}$ $= \dfrac{2}{−1} = −2$
$\lim\limits_{x\to a} \dfrac{f(x)}{g(x)}$ $= \dfrac{\lim\limits_{x\to a}f(x)}{\lim\limits_{x\to a}f(x)}$
Therefore:
$\lim\limits_{x\to 2} \dfrac{f(x)}{g(x)}$ $= \dfrac{\lim\limits_{x\to 2}f(x)}{\lim\limits_{x\to 2}f(x)}$ $= \dfrac{2}{−1} = −2$
Question 10 |
Identify the following limit using the graph below. Note that the graphs $f(x)$ and $g(x)$ are labeled by $f$ and $g$ respectively.
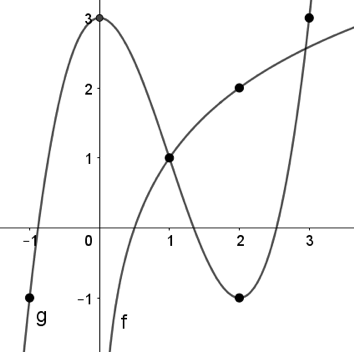 $\lim\limits_{x\to 3} f(g(x) − 2)$
$\lim\limits_{x\to 3} f(g(x) − 2)$
 $\lim\limits_{x\to 3} f(g(x) − 2)$
$\lim\limits_{x\to 3} f(g(x) − 2)$
$\text{Not enough information}$ | |
$2.5$ | |
$1$ | |
$0.5$ |
Question 10 Explanation:
The correct answer is (C). Composite functions are evaluated from the inside-out, meaning that we first evaluate the limit as $x$ approaches $3$ for the function $g(x) − 2$, the inner function of the composite.
Then, the limit evaluates to $g(3) − 2 = 3 − 2 = 1$ by direct substitution. Then, we evaluate the outer functions value at this output, meaning that we evaluate $f(1)$, which is $1$.
Therefore:
$\lim\limits_{x\to 3} f(g(x) − 2)$ $= f(g(3) − 2) = f(1) = 1$
Then, the limit evaluates to $g(3) − 2 = 3 − 2 = 1$ by direct substitution. Then, we evaluate the outer functions value at this output, meaning that we evaluate $f(1)$, which is $1$.
Therefore:
$\lim\limits_{x\to 3} f(g(x) − 2)$ $= f(g(3) − 2) = f(1) = 1$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
Derivatives Part 1 >>
AP Calculus Menu >>
