AP Calculus AB — Practice Exam Multiple Choice Part B

The correct answer is (A). Below is a portion of the graph of the revolved function.



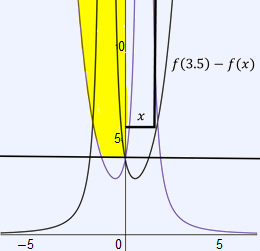
The shaded portion represents the portion of the graph that results from the revolution of the curve. Then, the radius is $x$, and the height is $f(3.5) − f(x)$. We must identify the other limit of $x$, which corresponds with intersection of $f(x)$ with $y = 4$. This occurs at $x = 0$ and $x = 1.12214412$.

However, the integral must be split into two portions. The first part is simply a rectangle, as all $f(x)$ values prior to $x = 1.2214412$ are all equal to $4$, by the bounds of the region. Then, the integral after that is dependent upon the function height.

We can identify the volume of the solid using shell method in the integral below.

$V=2π \displaystyle\int_0^{1.12214412} x(33.2636 − 4)dx~~+ $

$2π \displaystyle\int_{1.12214412}^{3.5}x(33.2636 − \dfrac{3}{(x+1)^2} − e^x) dx$

$≈ 737.01581$

The correct answer is (C). To find the acceleration function, we must derive the position function twice.

$s'(t) = v(t)$ $= \dfrac{1}{t^2} \cdot 2t + \dfrac{1}{\sin⁡(t)} \cdot \cos⁡(t)$ $= \dfrac{2}{t} + \cot⁡(t)$

$s''(t) = v'(t) = a(t)$ $= −\dfrac{2}{t^2} − \csc^2⁡(t)$

Then we can substitute $t = 7.6$

$a(7.6) = −\dfrac{2}{(7.6)^2} − \csc^2⁡ (7.6) ≈ −1.102$

The correct answer is (A). Begin by separating the variables:

$dy = \tan^2⁡(x) dx$

Integrate both sides to solve for $y$:

$y = \displaystyle\int \tan^2⁡(x) dx$

Since $\tan^2⁡(x) = \sec^2⁡(x) − 1$,

$y = \displaystyle\int (\sec^2(x) − 1) dx$

Splitting into two integrals and solving:

$y = \tan⁡(x) − x + C$

Using the initial value given:

$1 = \tan⁡(0) − 0 + C$

$C = 1$

Thus, the solution to the differential equation is:

$y = \tan⁡(x) − x + 1$

The correct answer is (A). Start by setting the equation equal and finding the bounds.

$\sqrt{x} = x^2$

$x = x^4$

$x^4 − x = 0$

$x(x^3 − 1) = 0$

$x = 0, 1$

On the interval $[0, 1]$, $f(x)$ is above $g(x)$ (using a graphing calculator). This means the integral to evaluate is:

$\displaystyle\int_0^1(\sqrt{x} − x^2)dx$

$\dfrac{2}{3} x^{\frac{3}{2}} − \dfrac{1}{3}x^3$

Applying the first fundamental theorem using the bounds:

$\left[ \dfrac{2}{3} (1)^{\frac{3}{2}} − \dfrac{1}{3}(1)^3 \right]$ $− \left[\dfrac{2}{3} (0)^{\frac{3}{2}} − \dfrac{1}{3}(0)^3 \right]$

$= \dfrac{2}{3} − \dfrac{1}{3} − 0 = \dfrac{1}{3}$

The correct answer is (C). To find the number of critical points, we must identify the function’s critical points. We do this by finding the derivative of the function and setting it equal to zero.

$f'(x) =$ $ x^4 + x^2 − 7x^2 − x + 6 = 0$

Using the calculator, we find that the function has roots $x = −2$, $x = −1.3027$, $x = 1$, and $x = 2.3027$. Therefore, the function has $4$ critical points.

The correct answer is (C). The velocity function is equal to $\frac{dy}{dx}$. Recall that the first derivative of two parametric equations has the formula below.

$\dfrac{dy}{dx} = \dfrac{\frac{dy}{dt}}{\frac{dx}{dt}}$

$\dfrac{dy}{dt} = 20 \cdot \cos⁡(\sqrt{t}) \cdot \dfrac{1}{2}(t)^{−\frac{1}{2}}$ $= \dfrac{10 \cos⁡(\sqrt{t})}{\sqrt{t}}$

$\dfrac{dx}{dt} = 3$

$\dfrac{dy}{dt}$ $= \dfrac{10 \cos⁡(\sqrt{t})}{3\sqrt{t}} = 0$

Solving for $t$, we find that $t = \left( \dfrac{π}{2} \right)^2 ≈ 2.467$ and $t = \left( \dfrac{3π}{2} \right)^2 ≈ 22.2066$, both of which are within the first $25$ seconds.

The correct answer is (C). The integral to be evaluated is:

$\dfrac{1}{5 − 1} \displaystyle\int_1^5 e^x dx$

$= \dfrac{1}{4} e^x$

Applying the first fundamental theorem:

$\dfrac{1}{4}e^5 − \dfrac{1}{4}e^1 = 36.424$

The correct answer is (B). To identify the acceleration of the particle, we must take the derivative of the position function twice.

$s'(x) = v(x)$ $= \dfrac{1}{x^3 + \cos⁡(x)} \cdot (3x^2 − sin⁡(x))$

$= \dfrac{(3x^2 − \sin⁡(x))}{x^3 + \cos⁡(x)}$


$s''(x) = v'(x) = a(x) =$

$\dfrac{(x^3 + \cos⁡(x))(6x − \cos⁡(x)) − (3x^2 − \sin⁡(x))(3x^2 − sin⁡(x))}{(x^3 + \cos⁡(x))^2}$

To save time on the examination, it is recommended that you do not simplify the above derivative. We can instead just evaluate the acceleration at $x = 3$ directly. This is where the calculator comes in handy.

$a(3) ≈ −0.33623$

The correct answer is (A). The limit evaluates to $\frac{\infty}{\infty}$ by direct substitution, which is one of the indeterminate forms that justifies the use of L’Hôpital’s rule.

It is important to recognize that the derivative of $2^n$ is $\ln⁡(2) \cdot 2^n$.

$\lim\limits_{n\to \infty} ⁡\dfrac{n^2}{2^n}$ $= \lim\limits_{n\to \infty} ⁡\dfrac{2n}{\ln(2) \cdot 2^n}$ $= \dfrac{\infty}{\infty}$

We can use L’Hôpital’s rule once again. Be careful with your derivation. The use of logarithmic rules will largely help in the derivation.

$\lim\limits_{n\to \infty} ⁡\dfrac{2n}{\ln(2) \cdot 2^n}$ $= \lim\limits_{n\to \infty} ⁡\dfrac{2}{(\ln(2))^2 \cdot 2^n} = 0$

The correct answer is (A). To find the equation of the tangent line, we must first identify the slope of the tangent line by identifying the derivative of the function at $x = 3$. Be careful with you derivation. Double product rule is necessary for derivation.

$f'(x) = $

$x \left( \ln⁡(10x) \cos⁡(x) + \sin⁡(x) \cdot \frac{1}{x} \right) + (\ln⁡(10x) \sin⁡(x))$

$= x \cdot \ln⁡(10x) \cos⁡(x) + \sin⁡(x) + \ln⁡(10x) \sin⁡(x)$


$f'(3) = $

$3 \cdot \ln⁡(30) \cos⁡(3) + \sin⁡(3) + \ln⁡(30) \sin⁡(3) ≈ −9.4804$

Then, we can identify the point of tangency for point-slope form by plugging in $x = 3$ into the original function.

$f(3) = 3 \ln⁡(30) \sin⁡(3) ≈ 1.4399$

Therefore, the point slope equation of the tangent line is of the form below.

$y − 1.4399 = −9.4804(x − 3)$

The correct answer is (D). We can relate the volume to the radius of a sphere using the formula for the volume of a sphere.

$V = \dfrac{4}{3} πr^3$

We can then derive this formula to relate the given rates.

$\dfrac{dV}{dt} = 4πr^2 \cdot \dfrac{dr}{dt}$

We were given that the balloon is being filled with $4$ cm$^3$ volume of air per minute. We are also given that the time is $2.25$ minutes. This means that $2.25(4) = 9$ cm$^3$ volume is present in the balloon at $2.25$ minutes. Thus, we can calculate the volume of the balloon at that time using the formula of the volume of a sphere:

$9 = \dfrac{4}{3} πr^3$

$r = \left(\dfrac{27}{4π} \right)^{\frac{1}{3}} ≈ 1.2904$

Then, we can solve for the rate of change of the radius by plugging in all the known values.

$4 = 4π(1.2904)^2 ⋅ \dfrac{dr}{dt}$

$\dfrac{dr}{dt} ≈ 0.1912$

The correct answer is (A). Below is a diagram of the scenario described by the problem.



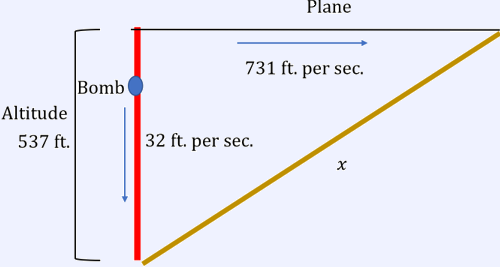
It is clear from the diagram that the relationship is related to triangle properties. We can relate the bombs height from the dropping altitude and the plane’s distance from the bomb with Pythagorean’s Theorem.

$a^2 + b^2 = c^2$

This implies that $a =$ altitude and $b =$ the planes distance from the bomb and $c =$ the distance between the two.

We can identify the distance the plane is from the bomb when it lands based on the rate of fall of the bomb. If the bomb has to travel $537$ feet to reach the ground, and it approaches the ground at a rate of $32$ feet per second, then it must take $\frac{537}{32} = 16.78125$ seconds for the bomb to reach the ground.

This implies that the plane has traveled $731(16.78125)$ $= 12267.094$ feet since dropping the bomb. This means that the distance between the plane and the bomb can be determined by substituting these values into the Pythagorean relationship.

$(537)^2 + (12267.094)^2 = x^2$

$x = 12278.842$

We can then relate the rates of the two objects by deriving the Pythagorean relationship.

$2a \cdot \dfrac{da}{dt} + 2b \cdot \dfrac{db}{dt}$ $= 2x \cdot \dfrac{dx}{dt}$

$2(537)(32) + 2(12267.094)(731)$ $= 2(12278.842) \cdot \dfrac{dx}{dt}$

$\dfrac{dx}{dt} ≈ 731.7$

The correct answer is (D). The position function of the particle is found by integrating the velocity function.

$s(t) = \displaystyle\int v(t) dt$ $=\displaystyle\int \sin⁡(\ln⁡(t))^2) dt$

At this point, actually integrating by hand is inefficient. This is where the calculator comes in handy. We can identify limits of integration to be $1$ to $3$ based on the given information. The position of the particle at $t = 3$ is then of the form below.

$s(3) = \displaystyle\int_1^3 \sin⁡(\ln⁡(t))^2) dt + 0$ $≈ 0.91377$

The correct answer is (C). The displacement of a particle along a position function has the formula below.

Displacement $= \displaystyle\int_a^b v(t)dt$

We can find the velocity function by deriving the position function. Be careful with your derivation.

$s'(t) = v(t) = \ln⁡(4) \cdot 4^x$

We can then plug this into the integral below.

$\displaystyle\int_1^{4.3} \ln⁡(4) \cdot 4^x dx ≈ 384.023$

The correct answer is (A). Recall that the first derivative of two parametric equations has the formula below.

$\dfrac{dy}{dx} = \dfrac{\frac{dy}{dt}}{\frac{dx}{dt}}$

We can find the slope of the tangent line at $t = 6$ based on the first derivative of the two functions.

$\dfrac{dx}{dt} = 8t \cdot \cos⁡(t^2)$

$\dfrac{dy}{dt} = e^t + 2t$

$\dfrac{dy}{dx} = \dfrac{e^t + 2t}{8t \cdot \cos⁡(t^2)}$

Then, we can substitute $t = 6$ into the equation.

$\dfrac{dy}{dx} = \dfrac{e^6 + 2(6)}{8(6) \cdot \cos⁡(6^2)}$ $≈ −67.635$