Below is our AP Calculus AB unit test on Riemann sums, trapezoidal sums, and average value of functions. These questions involve breaking down an integral into simple geometric shapes that can be used to calculate the area under a function. A majority of these problems require the memorization of a simple formula, which can then be used to find an approximation for the area under a curve.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Use a right Riemann sum with $4$ sub-intervals to estimate:
$\displaystyle\int_0^4 (x^4 + 5)dx$
$113$ | |
$261$ | |
$374$ | |
$379$ |
Question 1 Explanation:
The correct answer is (C). The interval we are computing the right Riemann sum on is $[0, 4]$. Since there are $4$ sub-intervals, we know that:
$Δx = \dfrac{4 − 0}{4} = 1$
The outputs for $0$, $1$, $2$, $3$, $4$ are shown in the table below:
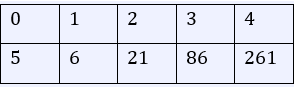
We can take the sum of the values on the right of each sub-interval, or the sum of the outputs of $1$,$2$,$3$, and $4$. This sum is $6 + 21 + 86 + 261 = 374$.
$Δx = \dfrac{4 − 0}{4} = 1$
The outputs for $0$, $1$, $2$, $3$, $4$ are shown in the table below:

We can take the sum of the values on the right of each sub-interval, or the sum of the outputs of $1$,$2$,$3$, and $4$. This sum is $6 + 21 + 86 + 261 = 374$.

Question 2 |
Use a left Riemann sum with $3$ sub-intervals to estimate:
$\displaystyle\int_0^{\frac{3π}{2}} \cos(x)dx$
$−1$ | |
$0$ | |
$1$ | |
$π$ |
Question 2 Explanation:
The correct answer is (B). The interval we are computing the left Riemann sum on is $\left[0, \frac{3π}{2}\right]$. Since there are $3$ sub-intervals, we know that:
$Δx = \dfrac{\frac{3π}{2} − 0}{3} = \dfrac{π}{2}$
The outputs for $0$, $\frac{π}{2}$, $π$, $\frac{3π}{2}$ are shown in the table below:
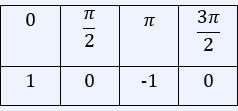
We can take the sum of the values on the left of each sub-interval, or the sum of the outputs of $0$, $\frac{π}{2}$, and $π$. This sum is $1 + 0 + (−1) = 0$.
$Δx = \dfrac{\frac{3π}{2} − 0}{3} = \dfrac{π}{2}$
The outputs for $0$, $\frac{π}{2}$, $π$, $\frac{3π}{2}$ are shown in the table below:

We can take the sum of the values on the left of each sub-interval, or the sum of the outputs of $0$, $\frac{π}{2}$, and $π$. This sum is $1 + 0 + (−1) = 0$.

Question 3 |
Use a Midpoint Riemann sum with $2$ sub-intervals to estimate:
$\displaystyle\int_0^4 (x^2 + 1)dx$
$4$ | |
$10$ | |
$12$ | |
$24$ |
Question 3 Explanation:
The correct answer is (D). Since there are $2$ sub-intervals:
$Δx = \dfrac{4 − 0}{2} = 2$
The table below shows the outputs for the function at $0$, $1$, $2$, $3$, and $4$.
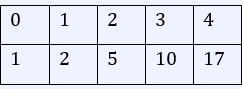
The midpoint of the interval $[0, 2]$ is $1$, and the midpoint of $[2, 4]$ is $3$. The sum of the outputs of $1$ and $3$ is $12$. Since $Δx$ is $2$, the final answer is $2 \cdot 12 = 24$.
$Δx = \dfrac{4 − 0}{2} = 2$
The table below shows the outputs for the function at $0$, $1$, $2$, $3$, and $4$.

The midpoint of the interval $[0, 2]$ is $1$, and the midpoint of $[2, 4]$ is $3$. The sum of the outputs of $1$ and $3$ is $12$. Since $Δx$ is $2$, the final answer is $2 \cdot 12 = 24$.

Question 4 |
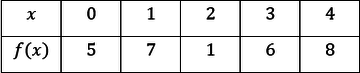
Use the following table to calculate a right Riemann sum on the interval $[0, 4],$ $ (Δx = 1)$.

$19$ | |
$22$ | |
$44$ | |
$66$ |
Question 4 Explanation:
The correct answer is (B). The right Riemann sum consists of the outputs at the end of each interval of length $1$. This is the sum of the outputs at $1$, $2$, $3$, and $4$. Therefore the Riemann sum is $7 + 1 + 6 + 8 = 22$.
Question 5 |
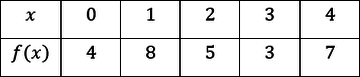
Use the following table to calculate a left Riemann sum on the interval $[0, 4],$ $ (Δx = 1)$.

$20$ | |
$23$ | |
$26$ | |
$29$ |
Question 5 Explanation:
The correct answer is (A). The left Riemann sum consists of the outputs at the beginning of each interval of length $1$. This is the sum of the outputs of $0$, $1$, $2$, and $3$. Therefore the left Riemann sum is $4 + 8 + 5 + 3 = 20$.
Question 6 |
Use the following table to calculate a midpoint Riemann sum on the interval $[0, 6],$ $n = 3$.


$15$ | |
$30$ | |
$45$ | |
$60$ |
Question 6 Explanation:
The correct answer is (B). The three intervals are $[0, 2]$, $[2, 4]$, $[4, 6]$. The corresponding outputs for the midpoint of each interval are $8$, $3$, and $4$. The sum of these three outputs, times the length of each interval, is $2(8 + 3 + 4) = 30$.
Question 7 |
Use a trapezoidal sum to approximate the area under the curve for the function $f(x) = 3x^2$ on the interval $[0, 6]$ with $n = 6$.
$48.5$ | |
$109.5$ | |
$219$ | |
$438$ |
Question 7 Explanation:
The correct answer is (C). The table below shows the outputs of the function at $0$, $1$, $2$, $3$, $4$, $5$, and $6$.
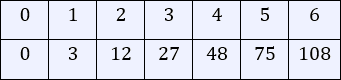
The general trapezoidal sum formula for equal sub-intervals is as follows:
$\dfrac{Δx}{2} [f(a) + 2f(a + Δx)~+ $ $2f(a + 2Δx) + ⋯ + f(b)]$
Plugging in the values from the table into the trapezoidal sum formula:
$\dfrac{1}{2} [0 + 2(3) + 2(12) + 2(27)~+ $ $2(48) + 2(75) + 108] = 219$

The general trapezoidal sum formula for equal sub-intervals is as follows:
$\dfrac{Δx}{2} [f(a) + 2f(a + Δx)~+ $ $2f(a + 2Δx) + ⋯ + f(b)]$
Plugging in the values from the table into the trapezoidal sum formula:
$\dfrac{1}{2} [0 + 2(3) + 2(12) + 2(27)~+ $ $2(48) + 2(75) + 108] = 219$
Question 8 |
Use a trapezoidal sum to approximate the area under the curve for the function $f(x) = x^5 − x^2$ on the interval $[0, 4]$ with $n = 4$.
$766$ | |
$1532$ | |
$1270$ | |
$1720$ |
Question 8 Explanation:
The correct answer is (A). The table below shows the outputs of the function at $0$, $1$, $2$, $3$ and $4$.
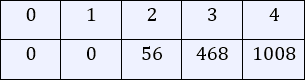
The general trapezoidal sum formula for equal sub-intervals is as follows:
$\dfrac{Δx}{2} [f(a) + 2f(a + Δx)~+$ $2f(a + 2Δx) + ⋯ + f(b)]$
Plugging in the values from the table into the trapezoidal sum formula:
$\dfrac{1}{2} [0 + 2(0) + 2(56)~+$ $2(468) + 1008] = 766$

The general trapezoidal sum formula for equal sub-intervals is as follows:
$\dfrac{Δx}{2} [f(a) + 2f(a + Δx)~+$ $2f(a + 2Δx) + ⋯ + f(b)]$
Plugging in the values from the table into the trapezoidal sum formula:
$\dfrac{1}{2} [0 + 2(0) + 2(56)~+$ $2(468) + 1008] = 766$
Question 9 |
Find the average value of the function $f(x) = x^3 + 2x^2$ on the interval $[0, 5]$.
$\dfrac{575}{12}$ | |
$\dfrac{1325}{12}$ | |
$\dfrac{1725}{12}$ | |
$\dfrac{2150}{12}$ |
Question 9 Explanation:
The correct answer is (A). The value to be evaluated is:
$\dfrac{1}{5−0} \displaystyle\int_0^5(x^3 + 2x^2)dx$
Solving gives the following definite integral:
$\dfrac{1}{5} \left[\dfrac{1}{4} x^4 + \dfrac{2}{3} x^3 \right]$ on the interval $[0, 5]$.
=$\dfrac{1}{5} \left[\dfrac{1}{4} (5)^4 + \dfrac{2}{3} (5)^3 \right]$ $− \dfrac{1}{5} \left[\dfrac{1}{4} (0)^4 + \dfrac{2}{3} (0)^3 \right]$
$= \dfrac{1}{5} \left[\dfrac{625}{4} + \dfrac{250}{3}\right]$ $= \dfrac{125}{4} + \dfrac{50}{3}$
$= \dfrac{375 + 200}{7}$ $= \dfrac{575}{12}$
$\dfrac{1}{5−0} \displaystyle\int_0^5(x^3 + 2x^2)dx$
Solving gives the following definite integral:
$\dfrac{1}{5} \left[\dfrac{1}{4} x^4 + \dfrac{2}{3} x^3 \right]$ on the interval $[0, 5]$.
=$\dfrac{1}{5} \left[\dfrac{1}{4} (5)^4 + \dfrac{2}{3} (5)^3 \right]$ $− \dfrac{1}{5} \left[\dfrac{1}{4} (0)^4 + \dfrac{2}{3} (0)^3 \right]$
$= \dfrac{1}{5} \left[\dfrac{625}{4} + \dfrac{250}{3}\right]$ $= \dfrac{125}{4} + \dfrac{50}{3}$
$= \dfrac{375 + 200}{7}$ $= \dfrac{575}{12}$
Question 10 |
Find the average value of the function $f(x) = e^{2x} + 5$ on the interval $[0, 3]$.
$\frac{1}{6}e^6 + \frac{25}{6} + e^2$ | |
$\frac{1}{6}e^2 + e^6$ | |
$\frac{1}{6}e^6 + \frac{29}{6}$ | |
$\frac{1}{2}e^2 + \frac{1}{6}e^6$ |
Question 10 Explanation:
The correct answer is (C). The integral to be evaluated is:
$\dfrac{1}{3 − 0} \displaystyle\int_0^3(e^{2x} + 5)dx$
Using a simple $u$-substitution and the power rule, the integral is equal to:
$\dfrac{1}{3} \left(\dfrac{1}{2} e^{2x} + 5x \right) + C$
Evaluating the definite integral on the interval $[0, 3]$:
$\dfrac{1}{3} \left[\dfrac{1}{2} e^{2(3)} + 5(3) \right]$ $−\dfrac{1}{3} \left[\dfrac{1}{2} e^{2(0)} + 5(0) \right]$
$= \dfrac{1}{6} e^6 + 5 − \dfrac{1}{6}$
$= \dfrac{1}{6} e^6 + \dfrac{29}{6}$
$\dfrac{1}{3 − 0} \displaystyle\int_0^3(e^{2x} + 5)dx$
Using a simple $u$-substitution and the power rule, the integral is equal to:
$\dfrac{1}{3} \left(\dfrac{1}{2} e^{2x} + 5x \right) + C$
Evaluating the definite integral on the interval $[0, 3]$:
$\dfrac{1}{3} \left[\dfrac{1}{2} e^{2(3)} + 5(3) \right]$ $−\dfrac{1}{3} \left[\dfrac{1}{2} e^{2(0)} + 5(0) \right]$
$= \dfrac{1}{6} e^6 + 5 − \dfrac{1}{6}$
$= \dfrac{1}{6} e^6 + \dfrac{29}{6}$
Question 11 |
Find the average value of the function $f(x) = \sin(x)\cos(x)$ on the interval $\left[0, \frac{π}{2}\right]$.
$\dfrac{1}{π}$ | |
$\dfrac{1}{2π}$ | |
$−\dfrac{1}{π}$ | |
$−\dfrac{1}{2π}$ |
Question 11 Explanation:
The correct answer is (A). The integral to be evaluated is:
$\dfrac{1}{\frac{π}{2} −0} \displaystyle\int_0^{\frac{π}{2}} \sin(x) \cos(x)dx$
A simpler way to solve this integral is to rewrite the integrand as
$\frac{1}{2} \sin(2x)$. $\dfrac{2}{π} \cdot \dfrac{1}{2} \displaystyle\int_0^{\frac{π}{2}} \sin(2x)dx$
Performing a $u$-substitution:
$(−1) \cdot \dfrac{2}{π} \cdot {1}{2} \cdot{1}{2} \cdot \cos(2x)$
Applying the first fundamental theorem over the given bounds:
$−\dfrac{1}{2π} [\cos(π) − \cos(0)]$
$= −\dfrac{1}{2π}(−1 − 1)$
$= \dfrac{1}{π}$
$\dfrac{1}{\frac{π}{2} −0} \displaystyle\int_0^{\frac{π}{2}} \sin(x) \cos(x)dx$
A simpler way to solve this integral is to rewrite the integrand as
$\frac{1}{2} \sin(2x)$. $\dfrac{2}{π} \cdot \dfrac{1}{2} \displaystyle\int_0^{\frac{π}{2}} \sin(2x)dx$
Performing a $u$-substitution:
$(−1) \cdot \dfrac{2}{π} \cdot {1}{2} \cdot{1}{2} \cdot \cos(2x)$
Applying the first fundamental theorem over the given bounds:
$−\dfrac{1}{2π} [\cos(π) − \cos(0)]$
$= −\dfrac{1}{2π}(−1 − 1)$
$= \dfrac{1}{π}$
Question 12 |
Find the average value of the function $f(x) = \tan(x)$ on the interval $\left[ 0, \dfrac{π}{3}\right]$.
$−\dfrac{3}{π} \ln(2)$ | |
$\dfrac{3}{π} \ln \left(\dfrac{1}{2} \right)$ | |
$−\dfrac{3}{π} \ln \left(−\dfrac{1}{2}\right)$ | |
$\dfrac{3}{π} \ln(2)$ |
Question 12 Explanation:
The correct answer is (D). The integral to be evaluated is:
$\dfrac{1}{\frac{π}{3} − 0}$ $\displaystyle\int_0^{\frac{π}{3}} \tan(x)dx$
$= \dfrac{3}{π} [−\ln|\cos(x)| ]$
Applying the first fundamental theorem using the given bounds:
$\dfrac{3}{π} \left[−\ln \left| \cos \left(\dfrac{π}{3} \right) \right| − (−\ln |\cos(0)|) \right]$
$= \dfrac{3}{π} \left[−\ln \left(\dfrac{1}{2} \right) + \ln(1) \right]$
$= \dfrac{3}{π} \left[\ln(1) − \ln\left(\dfrac{1}{2}\right)\right]$
Using the log rule $\ln(a) − \ln(b) = \ln\left(\dfrac{a}{b}\right)$ we have:
$= \dfrac{3}{π} \left[\ln\left(\dfrac{1}{\frac{1}{2}}\right)\right]$
$= \dfrac{3}{π} \ln(2)$
$\dfrac{1}{\frac{π}{3} − 0}$ $\displaystyle\int_0^{\frac{π}{3}} \tan(x)dx$
$= \dfrac{3}{π} [−\ln|\cos(x)| ]$
Applying the first fundamental theorem using the given bounds:
$\dfrac{3}{π} \left[−\ln \left| \cos \left(\dfrac{π}{3} \right) \right| − (−\ln |\cos(0)|) \right]$
$= \dfrac{3}{π} \left[−\ln \left(\dfrac{1}{2} \right) + \ln(1) \right]$
$= \dfrac{3}{π} \left[\ln(1) − \ln\left(\dfrac{1}{2}\right)\right]$
Using the log rule $\ln(a) − \ln(b) = \ln\left(\dfrac{a}{b}\right)$ we have:
$= \dfrac{3}{π} \left[\ln\left(\dfrac{1}{\frac{1}{2}}\right)\right]$
$= \dfrac{3}{π} \ln(2)$
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 12 questions to complete.
|
List |
Next Practice Test:
Trigonometric Integrals >>
AP Calculus Menu >>
