This is the first in our series of free SAT Math practice tests. It is based on the fourth section of the SAT, in which you are allowed to use a calculator. The SAT Math test went through a major revision in 2016, changing the focus to real world problems. Questions now include problems you might encounter at work, in your daily life, or in your college math and science courses. Try our SAT Math multiple choice questions to see if you are fully prepared for this section of the test.
The use of a calculator is allowed. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
There are 5 pencil-cases on the desk. Each pencil-case contains at least 10 pencils, but not more than 14 pencils. Which of the following could be the total number of pencils in all 5 cases?
35 | |
45 | |
65 | |
75 |
Question 1 Explanation:
If all pencil-cases have 10 pencils (the minimum number of pencils every pencil-case can hold), then the total minimum number of pencils is 10 × 5 = 50 pencils. Likewise, if all pencil-cases have 14 pencils (the maximum number of pencils every pencil-case can hold), then the total maximum number of pencils is 14 × 5 = 70 pencils. Thus, the answer must be between 50 and 70. Out of all the possible answer choices, only (C), 65 pencils, matches these criteria.
Question 2 |
A bird traveled 72 miles in 6 hours flying at constant speed. At this rate, how many miles did the bird travel in 5 hours?
12 | |
30 | |
60 | |
14.4 |
Question 2 Explanation:
First calculate the rate that the bird is traveling at:
$\frac{72 \text{ miles}}{6 \text{ hours}} = 12 \text{ miles per hour}$
The distance traveled in 5 hours will be:
$12 \text{ mph} * 5 \text{ h} = 60 \text{ miles}$
$\frac{72 \text{ miles}}{6 \text{ hours}} = 12 \text{ miles per hour}$
The distance traveled in 5 hours will be:
$12 \text{ mph} * 5 \text{ h} = 60 \text{ miles}$
Question 3 |
Three kids own a total of 96 comic books. If one of the kids owns 16 of the comic books, what is the average (arithmetic mean) number of comic books owned by the other two kids?
40 | |
42 | |
44 | |
46 |
Question 3 Explanation:
If one kid owns 16 of the comic books, then the number of comic books owned by the other two kids is: 96 − 16 = 80.
Therefore, the average is: 80 ÷ 2 = 40.
Therefore, the average is: 80 ÷ 2 = 40.
Question 4 |
If David has twice as many nickels as Tom, and Tom has 15 more nickels than John, what is the value in dollars of David’s nickels if John has 6 nickels?
$2.10 | |
$1.40 | |
$42.00 | |
$21.00 |
Question 4 Explanation:
If John has 6 nickels, then Tom has 15 + 6 = 21 nickels. If David has twice as many nickels as Tom, then David has 21 × 2 = 42 nickels. A nickel is worth 5 cents, so 42 nickels will be worth 42 × 5 = 210 cents. Because every dollar is worth 100 cents, this is equivalent to: $\dfrac{210}{100}$ = 2.1 dollars.
Question 5 |
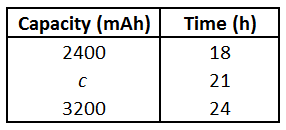
The table above shows the linear relationship between the capacity of a device's battery and the length of time it can be used before it must be recharged. What battery capacity, c, would be expected to provide 21 hours of usage?
2700 | |
2800 | |
2900 | |
3000 |
Question 5 Explanation:
Because the relationship is linear, we know that the rate of change is constant. The easiest way to make use of this knowledge is to notice that 21 is halfway between 18 and 24. This means that the number, c, we are looking for will be halfway between 2400 and 3200.
“Halfway” will be the mean (“average”) of these numbers:
$\dfrac{2400 + 3200}{2} = 2800~mAh$
“Halfway” will be the mean (“average”) of these numbers:
$\dfrac{2400 + 3200}{2} = 2800~mAh$
Question 6 |
The sum of two positive integers is 13. The difference between these numbers is 7. What is their product?
12 | |
22 | |
30 | |
40 |
Question 6 Explanation:
Use the given information to create a system of equations in two variables and then solve with the method of combination. Translating the problem statement into algebra:
$x + y = 13$
$x − y = 7$
Add the 2 equations together:
$x + x = 13 + 7;$
Now solve for $x$:
$2x = 20; \, x = 10$
The value of $y$ can then be found by plugging $x$ back into either of the two original equations:
$10 + y = 13; \, y = 3$
Once the variable values are found, their product can be computed:
$x * y = 10 * 3 = 30$
$x + y = 13$
$x − y = 7$
Add the 2 equations together:
$x + x = 13 + 7;$
Now solve for $x$:
$2x = 20; \, x = 10$
The value of $y$ can then be found by plugging $x$ back into either of the two original equations:
$10 + y = 13; \, y = 3$
Once the variable values are found, their product can be computed:
$x * y = 10 * 3 = 30$
Question 7 |
What is the difference between the median and the mode in the following set of data?
72, 44, 58, 32, 34, 68, 94, 22, 67, 45, 580 | |
2 | |
4 | |
6 |
Question 7 Explanation:
Start by organizing the data numerically from least to greatest:
22, 32, 34, 44, 45, 58, 58, 67, 68, 72, 94
The mode, or data value that occurs most often, is 58.
The median, or data value in the middle of the data set, is also 58.
The difference between these values is 0.
22, 32, 34, 44, 45, 58, 58, 67, 68, 72, 94
The mode, or data value that occurs most often, is 58.
The median, or data value in the middle of the data set, is also 58.
The difference between these values is 0.
Question 8 |
You are in charge of buying T-shirts for your school’s math club. There are 27 club members, who will each receive a shirt. The T-shirts come in boxes. Each box contains 4 T-shirts and costs \$23.50. What is the total cost for the T-shirts?
$164.50 | |
$634.50 | |
$141.00 | |
$150.65 |
Question 8 Explanation:
There are 27 club members, and each will receive a T-shirt. Each box contains 4 shirts, so:
$\dfrac{27}{4} = 6.75 → 7$
7 boxes of T-shirts will be ordered (since a whole number of boxes must be ordered). Each box costs \$23.50, so the total cost for all the shirts is:
$7 × \$23.50 = \$164.50$
$\dfrac{27}{4} = 6.75 → 7$
7 boxes of T-shirts will be ordered (since a whole number of boxes must be ordered). Each box costs \$23.50, so the total cost for all the shirts is:
$7 × \$23.50 = \$164.50$
Question 9 |
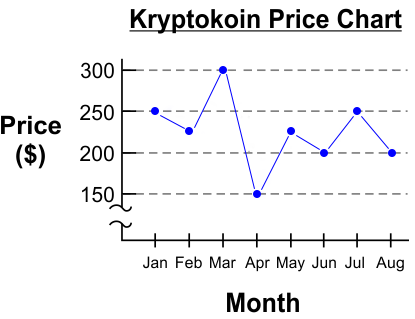
The price of Kryptokoin over an 8 month period is shown in the illustration. Paul takes cash from his shoebox and buys 10 of the coins in April. Three months later he sells 5 of the coins, and in August he sells the remaining 5 coins. He puts the cash from each of these sales back in the shoebox. Assuming no other cash was taken or added, by what amount has the cash in the shoebox increased?
$2250 | |
$750 | |
$1250 | |
$450 |
Question 9 Explanation:
Bought 10 coins in April:
Price in April = \$150/coin
Cash spent = (10 coins)(\$150/coin) = \$1500
Sold 5 coins in July (3 Months Later):
Price in July = \$250/coin
Cash received = (5 coins)(\$250/coin) = \$1250
Sold 5 coins in August:
Price in August = \$200/coin
Cash received = (5 coins)(\$200/coin) = \$1000
Assuming he had \$T of cash in the shoebox to start with:
\$T − \$1500 + \$1250 + \$1000
\$T + \$750
Cash has increased by \$750.
Price in April = \$150/coin
Cash spent = (10 coins)(\$150/coin) = \$1500
Sold 5 coins in July (3 Months Later):
Price in July = \$250/coin
Cash received = (5 coins)(\$250/coin) = \$1250
Sold 5 coins in August:
Price in August = \$200/coin
Cash received = (5 coins)(\$200/coin) = \$1000
Assuming he had \$T of cash in the shoebox to start with:
\$T − \$1500 + \$1250 + \$1000
\$T + \$750
Cash has increased by \$750.
Question 10 |
Every May, Robo Carwash offers a “Buy 4 Get 2 Free” promotion—for every 4 carwash tickets purchased at $8 per ticket, the customer receives 2 additional carwash tickets for free. What is the true cost per carwash ticket for a customer who takes advantage of the promotion?
$6.00 | |
$5.33 | |
$4.00 | |
$6.67 |
Question 10 Explanation:
True Cost per carwash ticket = $\frac{\text{Total Cost}}{\text{Number of Carwash Tickets}}$
Total cost = (\$8 per ticket)(4 tickets)
= \$32
Number of Carwash Tickets = 4 (paid for) + 2 (free)
=6 tickets
True Cost per carwash = $\frac{\$8}{6 \text{ Tickets}}$
= \$5.33 per carwash ticket
Total cost = (\$8 per ticket)(4 tickets)
= \$32
Number of Carwash Tickets = 4 (paid for) + 2 (free)
=6 tickets
True Cost per carwash = $\frac{\$8}{6 \text{ Tickets}}$
= \$5.33 per carwash ticket
Question 11 |
Approximately 4 out of every 25,000 males has a genetic mutation resulting in hemophilia. Approximately how many male Americans would be expected to have this genetic mutation if the current male population of America is 163 million?
41,000 | |
1,019,000 | |
65,000 | |
26,000 |
Question 11 Explanation:
Set up equivalent proportions:
$\dfrac{x \text{ have mutation}}{163{,}000{,}000 \text{ males}}$ $= \dfrac{4 \text{ have mutation}}{25{,}000 \text{ males}}$
Cross multiply to solve for $x$:
$(25{,}000)(x)$ $= (4)(163{,}000{,}000)$
$x = \frac{(4)(163{,}000{,}000)}{25{,}000}$
$x = 26{,}080 \approx 26{,}000$
$\dfrac{x \text{ have mutation}}{163{,}000{,}000 \text{ males}}$ $= \dfrac{4 \text{ have mutation}}{25{,}000 \text{ males}}$
Cross multiply to solve for $x$:
$(25{,}000)(x)$ $= (4)(163{,}000{,}000)$
$x = \frac{(4)(163{,}000{,}000)}{25{,}000}$
$x = 26{,}080 \approx 26{,}000$
Question 12 |
You've been tasked with creating the rectangular pen (fenced-in area) shown above using a maximum of 300 m of fence. The pen must have an area of at least 5400 m2. What set of inequalities should be used to best describe the requirements?
$2l + 2 w ≤ 300$ $l \cdot w ≥ 5400$ | |
$l + w ≤ 300$ $l \cdot w ≤ 5400$ | |
$2l + 2 w ≤ 300$ $2l \cdot 2w ≥ 5400$ | |
$l + w ≤ 300$ $2l \cdot 2w ≥ 5400$ |
Question 12 Explanation:
Perimeter is simply the distance around an object. In this case:
$P = l + w + l + w$
$P = 2l + 2w$
P must be a maximum of 300 m, meaning it must be less than or equal to 300 m:
$P ≤ 300$
$2l + 2 w ≤ 300$
The Area of a rectangle is:
$A = l \cdot w$
The area must be at least 5400 m2:
$A ≥ 5400$
$l \cdot w ≥ 5400$
$P = l + w + l + w$
$P = 2l + 2w$
P must be a maximum of 300 m, meaning it must be less than or equal to 300 m:
$P ≤ 300$
$2l + 2 w ≤ 300$
The Area of a rectangle is:
$A = l \cdot w$
The area must be at least 5400 m2:
$A ≥ 5400$
$l \cdot w ≥ 5400$
Question 13 |
The vertex of a parabolic function is located at (5,−4). One of its zeros (x-intercepts) occurs at $x$ = 7. Where will its other zero (x-intercept) be located?
$x = 12$ | |
$x = 3$ | |
$x = 0$ | |
$x = 9$ |
Question 13 Explanation:
We have been given the vertex and one of the zeros of the parabolic function (i.e. a parabola that either opens up or down)
If one of the zeros lies 2 units (horizontally) to the right of the vertex, the other zero will lie 2 units (horizontally) to the left. This means the other zero will be located at $x$ = 3 (3, 0)
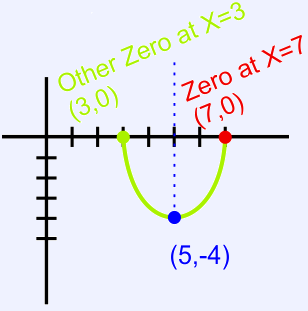
If one of the zeros lies 2 units (horizontally) to the right of the vertex, the other zero will lie 2 units (horizontally) to the left. This means the other zero will be located at $x$ = 3 (3, 0)
Question 14 |
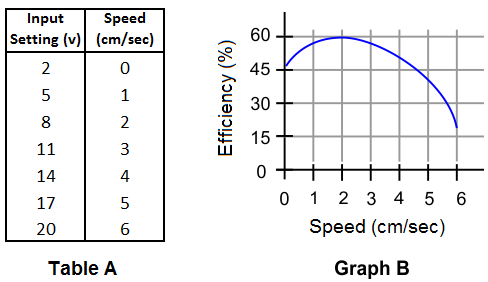
Table A shows the Speed of a vehicle as a function of an “Input Setting”. Graph B shows the Efficiency of the same vehicle as a function of Speed. What “Input Setting” will result in the maximum Efficiency for this vehicle?
20 | |
8 | |
0 | |
2 |
Question 14 Explanation:
Looking at Graph B we see that the maximum efficiency of 60% occurs when Speed = 2 cm/sec. We need to determine the “Input Setting” that results in a speed of 2 cm/sec. Using Table A we can determine that an input setting of 8v will give us the desired speed.
Question 15 |
A “Triangle” is any positive integer greater than 1 that has only three positive integer factors: itself, its square root, and 1. Which of the following is a Triangle?
169 | |
100 | |
36 | |
81 |
Question 15 Explanation:
The only factors of 169 are: 169, 13, and 1. (The square root of 169 is 13.) All of the other options have more than 3 factors; or, put another way, the square roots of the other
answers (10, 6, and 9, respectively) are not prime numbers.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
List |
Next Practice Test:
SAT Math Practice Test 2 >>
SAT Main Menu >>