Try our second free SAT Math practice test. This one is a little more challenging, with a mixture of easy and medium level practice questions. You are permitted to use a calculator on this portion of the math test, but you won’t need it for every question. Topics include linear equations, inequalities, problem solving, and functions. Continue your test prep with these SAT Math practice problems.
The use of a calculator is allowed. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Franklin bought several kites, each costing 16 dollars. Richard purchased several different kites, each costing 20 dollars. If the ratio of the number of kites Franklin purchased to the number of kites Richard purchased was 3 to 2, what was the average cost of each kite they purchased?
$16.80 | |
$17.20 | |
$17.60 | |
$18.00 |
Question 1 Explanation:
For every 5 kites purchased by Franklin and Richard, 3 of the kites are Franklin’s and 2 of the kites are Richard’s. We can set up an equation to find the total money spent:
Total money spent for every 5 kites: 3(16) + 2(20) = 88
To find the average cost per kite, we can simply divide 88 by 5:
88 ÷ 5 = 17.6
Total money spent for every 5 kites: 3(16) + 2(20) = 88
To find the average cost per kite, we can simply divide 88 by 5:
88 ÷ 5 = 17.6
Question 2 |
Circle A is inside Circle B, and the two circles share the same center O. If the circumference of B is four times the circumference of A, and the radius of Circle A is three, what is the difference between Circle B’s diameter and Circle A’s diameter?
6 | |
9 | |
12 | |
18 |
Question 2 Explanation:
Start by drawing the figure.
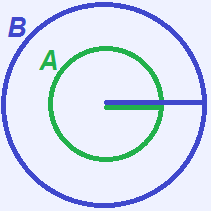
If the radius of A is 3, then its diameter is 6. Its circumference is 2πr = 2(3)π = 6π.
B’s circumference is four times A’s circumference.
B’s circumference = 4(6π) = 24π.
Now work backwards to find B's radius from its circumference:
24π = 2πr, so B’s radius must be 12. Its diameter is then 12 * 2 = 24.
The difference between the diameters is then: 24 – 6 = 18.

If the radius of A is 3, then its diameter is 6. Its circumference is 2πr = 2(3)π = 6π.
B’s circumference is four times A’s circumference.
B’s circumference = 4(6π) = 24π.
Now work backwards to find B's radius from its circumference:
24π = 2πr, so B’s radius must be 12. Its diameter is then 12 * 2 = 24.
The difference between the diameters is then: 24 – 6 = 18.
Question 3 |
Line F can be described by the function ƒ(x) = 5x. Line G is parallel to Line F such that the shortest distance between Line G and Line F is c, and the y-intercept of Line G is negative. Which of the following is a possible equation for line G?
$g(x) = x - 5$ | |
$g(x) + 5\sqrt{2} = 5x$ | |
$g(x) = x - 5\sqrt{2}$ | |
$g(x) - 5 = 5x$ |
Question 3 Explanation:
Start by drawing the lines:
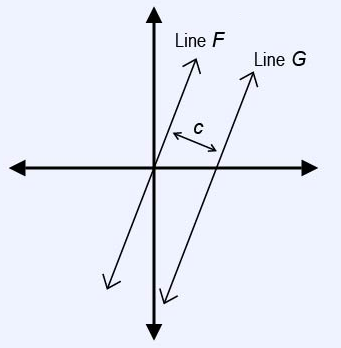
The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept. Parallel lines have the same slope, so Line G must also have a slope of 5. Therefore, we can eliminate choices (A) and (C).
Since the y-intercept of Line G must be negative, we can eliminate choice (D).
Thus, the answer is (B).

The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept. Parallel lines have the same slope, so Line G must also have a slope of 5. Therefore, we can eliminate choices (A) and (C).
Since the y-intercept of Line G must be negative, we can eliminate choice (D).
Thus, the answer is (B).
Question 4 |
VitaDrink contains 30 percent concentrated nutrients by volume. EnergyPlus contains 40 percent concentrated nutrients by volume. Which of the following represents the percentage of concentrated nutrients by volume in a mixture of $v$ gallons of VitaDrink, $e$ gallons of EnergyPlus, and $w$ gallons of water?
$\dfrac{v+e}{v+e+w}$
| |
$\dfrac{0.3v+0.4e}{v+e+w}$
| |
$\dfrac{3v+4e}{v+e+w}$
| |
$\dfrac{30v+40e}{v+e+w}$
|
Question 4 Explanation:
The total number of gallons in the final mixture will be the sum of all the components: $v $+ $e$ + $w$.
There are 0.3$v$ gallons of nutrients from VitaDrink in the mixture, 0.4$e$ gallons of nutrients from EnergyPlus in the mixture, and no nutrients from the water.
The total number of gallons of nutrients in the new mixture will be 0.3$v$ + 0.4$e$.
To convert from a fraction to a percent, we simply multiply our value by 100:
$100 * \dfrac{0.3v + 0.4e}{v + e + w}$
$= \dfrac{30v + 40e}{v + e + w}$
If you chose (B), remember that the question was asking for the percent, not the actual number in the mixture!
There are 0.3$v$ gallons of nutrients from VitaDrink in the mixture, 0.4$e$ gallons of nutrients from EnergyPlus in the mixture, and no nutrients from the water.
The total number of gallons of nutrients in the new mixture will be 0.3$v$ + 0.4$e$.
To convert from a fraction to a percent, we simply multiply our value by 100:
$100 * \dfrac{0.3v + 0.4e}{v + e + w}$
$= \dfrac{30v + 40e}{v + e + w}$
If you chose (B), remember that the question was asking for the percent, not the actual number in the mixture!
Question 5 |
$\dfrac{41}{12}$ | |
$\dfrac{41}{11}$ | |
$\dfrac{31}{9}$ | |
$\dfrac{31}{7}$ |
Question 5 Explanation:
Use the given information to relate the values on the left with the values on the right. Remember that if two lines are divided proportionally, the corresponding segments are in proportion and the two lines and either pair of corresponding segments are in proportion. Set up the proportion and solve for the unknown:
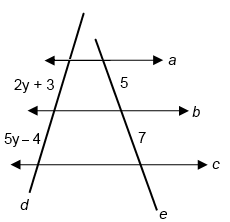
$\dfrac{2y + 3}{5y - 4} = \dfrac{5}{7}$
Cross multiply and combine like terms to solve for $y$:
$7(2y + 3) = 5(5y − 4)$
$14y + 21 = 25y − 20$
$41 = 11y$
$y = \dfrac{41}{11}$
$\dfrac{2y + 3}{5y - 4} = \dfrac{5}{7}$
Cross multiply and combine like terms to solve for $y$:
$7(2y + 3) = 5(5y − 4)$
$14y + 21 = 25y − 20$
$41 = 11y$
$y = \dfrac{41}{11}$
Question 6 |
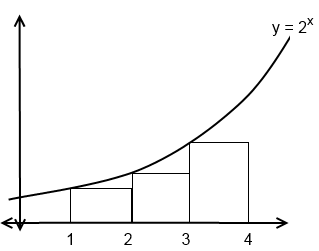
What is the sum of the areas of the three rectangles that are drawn below the graph of the line $y = 2^x$?
6 | |
12 | |
14 | |
16 |
Question 6 Explanation:
Start by plugging $x = 1$, $x = 2$, and $x = 3$ into the equation $y = 2^x$. This will determine the $y$-coordinates where the corner of each rectangle touches $y = 2^x$. Those $y$-values will be the height of each rectangle.
Since we know each rectangle is 1 space apart, we can then find each area.
The areas are:
$2(1) = 2$
$4(1) = 4$
$8(1) = 8$
Adding up the areas, we get: $2 + 4 + 8 = 14$
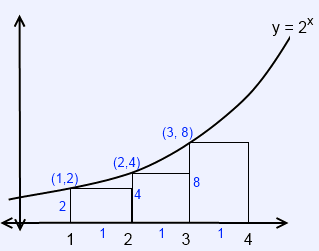
Since we know each rectangle is 1 space apart, we can then find each area.
The areas are:
$2(1) = 2$
$4(1) = 4$
$8(1) = 8$
Adding up the areas, we get: $2 + 4 + 8 = 14$

Question 7 |
If AB is parallel to DC, and AD is parallel to BC, then what is the value of $b − a$?

30° | |
50° | |
60° | |
70° |
Question 7 Explanation:
If AB is parallel to DC, then BD is a transversal. Alternate interior angles between two parallel lines cut by a transversal are equal.
$∠BDC = ∠ABD$, so $a = 30^{\circ}$.
The sum of the interior angles of a triangle is $180^{\circ}$, so we can write the equation below:
$a + b + 70^{\circ} = 180^{\circ}$
$a + b = 110^{\circ}$
$(30^{\circ}) + b = 110^{\circ}$
$b = 80^{\circ}$
Substitute the determined values and evaluate:
$b − a = 80^{\circ} − 30^{\circ} = 50^{\circ}$
$∠BDC = ∠ABD$, so $a = 30^{\circ}$.
The sum of the interior angles of a triangle is $180^{\circ}$, so we can write the equation below:
$a + b + 70^{\circ} = 180^{\circ}$
$a + b = 110^{\circ}$
$(30^{\circ}) + b = 110^{\circ}$
$b = 80^{\circ}$
Substitute the determined values and evaluate:
$b − a = 80^{\circ} − 30^{\circ} = 50^{\circ}$
Question 8 |
The speed of a subway train is represented by the equation $v = t^2 + 2t \,$ for all situations where $0 ≤ t ≤ 7$, where $v$ is the rate of speed in km per hour, and $t$ is the time in seconds from the moment the train starts moving.
In km per hour, how much faster is the subway train moving after 7 seconds than it was moving after 3 seconds?4 | |
9 | |
15 | |
48 |
Question 8 Explanation:
For this word problem, we are asked for the difference between the train’s speed after 7 seconds, and the train’s speed after 3 seconds.
First evaluate the function at $t$ = 7. From this value, evaluate the function at $t$ = 3, and then find the difference between the two:
$v(7) = (7)^2+ 2(7) = 63$
$v(3) = (3)^2 + 2(3) = 15$
$v(7) − v(3) = 63 − 15 = 48$
First evaluate the function at $t$ = 7. From this value, evaluate the function at $t$ = 3, and then find the difference between the two:
$v(7) = (7)^2+ 2(7) = 63$
$v(3) = (3)^2 + 2(3) = 15$
$v(7) − v(3) = 63 − 15 = 48$
Question 9 |
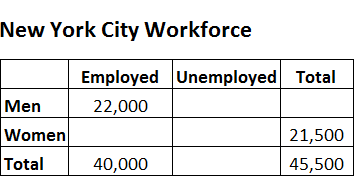
The table above, which describes the New York City workforce, is only partially filled. Based on this information, what proportion of the total New York City workforce are unemployed women?
$\dfrac{43}{91}$ | |
$\dfrac{7}{43}$ | |
$\dfrac{11}{91}$ | |
$\dfrac{1}{13}$ |
Question 9 Explanation:
First, we can compute the number of employed women by using the numbers in the first column:
40,000 − 22,000 = 18,000
Then, we can compute the number of unemployed women by using the data in the second row:
21,500 − 18,000 = 3,500
Thus, 3,500 women in the New York City workforce are unemployed.
To find the proportion of the total NYC workforce that are unemployed women, we setup the proportion:
$\frac{\text{Unemployed Women}}{\text{Total Workforce}} = \frac{3500}{45500}$
$= \frac{35}{455} = \frac{5 \ast 7}{5 \ast 91}$
$= \frac{7}{91} = \frac{1}{13}$
40,000 − 22,000 = 18,000
Then, we can compute the number of unemployed women by using the data in the second row:
21,500 − 18,000 = 3,500
Thus, 3,500 women in the New York City workforce are unemployed.
To find the proportion of the total NYC workforce that are unemployed women, we setup the proportion:
$\frac{\text{Unemployed Women}}{\text{Total Workforce}} = \frac{3500}{45500}$
$= \frac{35}{455} = \frac{5 \ast 7}{5 \ast 91}$
$= \frac{7}{91} = \frac{1}{13}$
Question 10 |
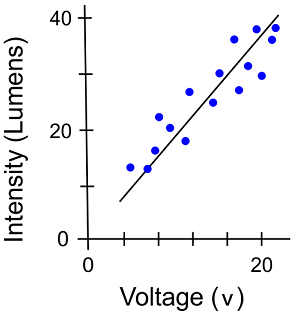
The figure shows the line of best fit through a set of experimental data. If the equation of the line of best fit is:
Intensity = 1.78 (Voltage) + 1.5 Which of the following input voltages would most likely result in an Intensity of 30 Lumens according to the line of best fit?15.3 $v$ | |
16.0 $v$ | |
20.0 $v$ | |
54.9 $v$ |
Question 10 Explanation:
Graphically it looks very close to 16 $v$. To confirm we can use basic algebra:
Intensity = 1.78 (Voltage) + 1.5
30 = 1.78 (Voltage) + 1.5
28.5 = 1.78 (Voltage)
16.011 = Voltage
Voltage = 16.0 is the best answer.
Intensity = 1.78 (Voltage) + 1.5
30 = 1.78 (Voltage) + 1.5
28.5 = 1.78 (Voltage)
16.011 = Voltage
Voltage = 16.0 is the best answer.
Question 11 |
What is one possible value of $x + 2$ for the equation below?
$\dfrac{1}{3x + 6} = \dfrac{x + 2}{48}$−6 | |
−2 | |
2 | |
−4 |
Question 11 Explanation:
This problem can be solved as shown below:
$\dfrac{1}{3x + 6} = \dfrac{x + 2}{48}$
$\dfrac{1}{3(x + 2)} = \dfrac{x + 2}{48}$
Cross multiply to get:
$48 = 3 (x + 2)(x + 2)$
$16 = (x + 2)^2$
$\pm \sqrt{16} = \sqrt{(x + 2)^2}$
$\pm4 = x + 2$
$\dfrac{1}{3x + 6} = \dfrac{x + 2}{48}$
$\dfrac{1}{3(x + 2)} = \dfrac{x + 2}{48}$
Cross multiply to get:
$48 = 3 (x + 2)(x + 2)$
$16 = (x + 2)^2$
$\pm \sqrt{16} = \sqrt{(x + 2)^2}$
$\pm4 = x + 2$
Question 12 |
A company uses an additive manufacturing (“3D Printing”) process to create square pyramids as shown in the illustration. If the 3D printer can print 0.025 cm3 per second, how many minutes will it take to print one pyramid?
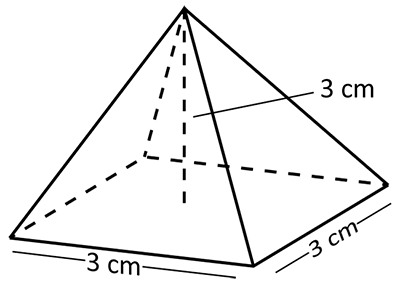
14 | |
9 | |
6 | |
18 |
Question 12 Explanation:
Start by calculating the volume of the pyramid:
$V = \frac{1}{3}(l \cdot w \cdot h)$
$= \frac{1}{3}(3 \cdot 3 \cdot 3) = 9 \text{ cm}^3$
$9~\require{cancel}\cancel{\text{ cm}^3} = \frac{1 \text{ sec}}{0.025~\cancel{\text{cm}^3}}$ $= 360 \text{ sec}$
$(or~\frac{0.025 \text{ cm}^3}{1 \text{ sec}} = \frac{9 \text{ cm}^3}{x \text{ sec}})$
$t = 360 \text{ sec}$
$360 \require{cancel}\cancel{\text{ sec}} \cdot \frac{1 \text{ min}}{60 \cancel{\text{ sec}}} = 6 \text{ min}$
$V = \frac{1}{3}(l \cdot w \cdot h)$
$= \frac{1}{3}(3 \cdot 3 \cdot 3) = 9 \text{ cm}^3$
$9~\require{cancel}\cancel{\text{ cm}^3} = \frac{1 \text{ sec}}{0.025~\cancel{\text{cm}^3}}$ $= 360 \text{ sec}$
$(or~\frac{0.025 \text{ cm}^3}{1 \text{ sec}} = \frac{9 \text{ cm}^3}{x \text{ sec}})$
$t = 360 \text{ sec}$
$360 \require{cancel}\cancel{\text{ sec}} \cdot \frac{1 \text{ min}}{60 \cancel{\text{ sec}}} = 6 \text{ min}$
Question 13 |
On a certain street there are 7 houses. The value of each of these houses is provided in the table below. An 8th house is being added on the same street and will have a value in excess of $255,000. What is the lowest value that this new home can have such that the mean of all 8 house values will be greater than or equal to the median of the 8 house values?
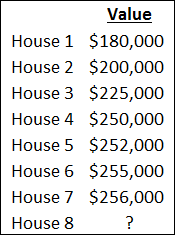
$390,000 | |
$502,000 | |
$415,000 | |
$276,000 |
Question 13 Explanation:
The median is the "middle" value in our list of 8 homes:

The mean will be the sum of all the values above along with the missing value, divided by the the total number of values:
$\bar{x} = \dfrac{1618 + x}{8}$ (in thousands of \$)
For the mean, $\bar{x}$, to be greater or equal to the median:
$\bar{x} \geq Median$
$\dfrac{1618 + x}{8} \geq 251$
$x \geq 390$
House 8 will cost \$390,000 or more.

The mean will be the sum of all the values above along with the missing value, divided by the the total number of values:
$\bar{x} = \dfrac{1618 + x}{8}$ (in thousands of \$)
For the mean, $\bar{x}$, to be greater or equal to the median:
$\bar{x} \geq Median$
$\dfrac{1618 + x}{8} \geq 251$
$x \geq 390$
House 8 will cost \$390,000 or more.
Question 14 |
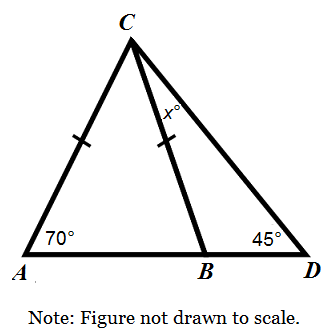
Triangle ABC is the isosceles triangle shown in the illustration below. ∠A = 70° and ∠D = 45°. Points A, B, and D are colinear. Find x, the measure of ∠BCD.
20° | |
15° | |
25° | |
30° |
Question 14 Explanation:
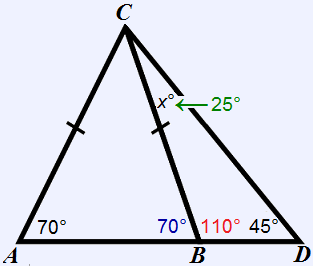
Since △ABC is isosceles, its base angles will be the same:
∠ABC = ∠BAC = 70°
Angles ∠ABC and ∠CBD form a linear pair — meaning they are supplementary (i.e. ∠ABC + ∠CBD = 180°).
∠ABC + ∠CBD = 180°
70° + ∠CBD = 180°
∠CBD = 110°
The angles of △BCD must add to 180°.
110° + 45° + x° = 180°
x = 25°
Question 15 |
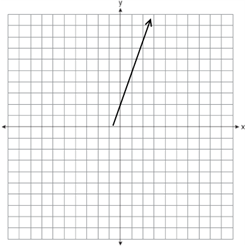
If (m,ƒ(m)) represents a point on the graph ƒ(m) = 2m + 1, which of the following could be a portion of the graph of the set of points (m,(ƒ(m))2)?
 | |
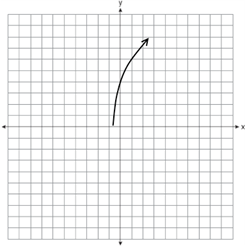 | |
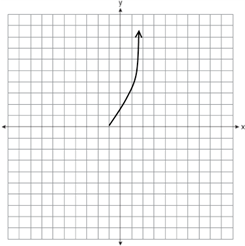 | |
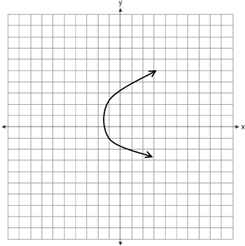 |
Question 15 Explanation:
Let’s re-write the “m” as an “x” to better understand how this function would look on an xy-coordinate plane.
Begin with the equation provided in the question, ƒ(m), and square it, ƒ(m)2:
ƒ(m) = 2x + 1
ƒ(m)2 = (2x + 1)2 = 4x2 + 4x + 1
By factoring out a 4 from the expression, the vertex form of the quadratic can be found:
4(x2 + x + $\frac{1}{4}$) = 4(x + $\frac{1}{2}$)2
The correct graph is (C). This function translates graphically into a parabola with a vertex at (−½, 0) that is vertically stretched and opens upwards. Only answer choice (C) shows an appropriate possibility.
Begin with the equation provided in the question, ƒ(m), and square it, ƒ(m)2:
ƒ(m) = 2x + 1
ƒ(m)2 = (2x + 1)2 = 4x2 + 4x + 1
By factoring out a 4 from the expression, the vertex form of the quadratic can be found:
4(x2 + x + $\frac{1}{4}$) = 4(x + $\frac{1}{2}$)2
The correct graph is (C). This function translates graphically into a parabola with a vertex at (−½, 0) that is vertically stretched and opens upwards. Only answer choice (C) shows an appropriate possibility.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
SAT Math Practice Test 3 >>
SAT Main Menu >>