This is the first of our No Calculator SAT Math practice tests. This is based on section 3 of the SAT, which includes a total of 20 questions. Our practice questions are sorted by difficulty level so that you can focus questions that challenge you. While this is our easiest test, it covers many important skills and includes some tricky problems. We recommend that all students start here.
The use of a calculator is NOT permitted. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
If $x$ is $6$ less than $y$, and $y$ is twice of $z$, what is the value of $x$ when $z = 2$ ?
10 | |
8 | |
−2 | |
12 |
Question 1 Explanation:
Let's set up some equations to solve for $x$. Translating from English to math, we get:
"$x$ is 6 less than $y$" ⇒ $x = y - 6$
"$y$ is twice of $z$" ⇒ $y = 2z$
Now plug in $z = 2$:
$y = 2z = 2(2) = 4$
$x = y - 6$
$x = 4 - 6$
$x = -2$
"$x$ is 6 less than $y$" ⇒ $x = y - 6$
"$y$ is twice of $z$" ⇒ $y = 2z$
Now plug in $z = 2$:
$y = 2z = 2(2) = 4$
$x = y - 6$
$x = 4 - 6$
$x = -2$
Question 2 |
If $x + 3 = y$, then $2x + 6 = \; ?$
$y$ | |
$2y$ | |
$3y$ | |
$4y$ |
Question 2 Explanation:
We can rewrite $x + 3 = y\,$ as $\,x = y - 3$
Plugging this value of $x$ into the 2nd equation, we get:
$2(y - 3) + 6$
Simplifying: $2y - 6 + 6 = 2y$
Therefore, $2y$ is the answer.
Alternatively, notice that $2x+6$ is just $2*(x+3)$. Thus, it must be equal to $2*y = 2y$.
Plugging this value of $x$ into the 2nd equation, we get:
$2(y - 3) + 6$
Simplifying: $2y - 6 + 6 = 2y$
Therefore, $2y$ is the answer.
Alternatively, notice that $2x+6$ is just $2*(x+3)$. Thus, it must be equal to $2*y = 2y$.
Question 3 |
$3(x - 4) = 18$, what is the value of $x$?
$\dfrac{14}{3}$
| |
$\dfrac{22}{3}$
| |
$6$ | |
$10$ |
Question 3 Explanation:
First, distribute the 3, then solve for $x$:
$3(x − 4) = 18$
$3x − 12 = 18$
$3x = 30$
$x = 10$
$3(x − 4) = 18$
$3x − 12 = 18$
$3x = 30$
$x = 10$
Question 4 |
Cecilia, Robbie, and Briony all bought stamps. The number of stamps Cecilia purchased was equal to a single digit. Only one of the three purchased a number of stamps that is divisible by 3. At least one of the three purchased an even number of stamps. Which of the following could represent the numbers of stamps each person purchased?
3, 8, 24 | |
7, 9, 17 | |
9, 10, 13 | |
6, 9, 12 |
Question 4 Explanation:
This can be solved with process of elimination. Since each of the answer choices has at least one single-digit number, let’s look at the second requirement. If the number of stamps that ONLY ONE of them purchased was divisible by 3, we can eliminate answer choices that contain more than one multiple of 3: (A) and (D).
The third requirement is that we have at least one even number. Between answers (B) and (C), only (C) satisfies this requirement.
The third requirement is that we have at least one even number. Between answers (B) and (C), only (C) satisfies this requirement.
Question 5 |
For their school uniform, each student can choose from 4 types of tops and 3 types of bottoms. How many combinations of tops and bottoms are there?
7 | |
12 | |
1 | |
10 |
Question 5 Explanation:
This is a simple probability question. For every top, there are 3 types of bottoms. We know that there are 4 types of tops.
Thus, there are 3 × 4 = 12 combinations of tops and bottoms.
Thus, there are 3 × 4 = 12 combinations of tops and bottoms.
Question 6 |
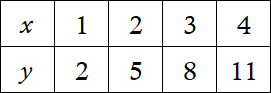
The table above represents a relationship between and $x$ and $y$. Which of the following linear equations describes the relationship?
$y = x + 3$ | |
$y = 3x - 1$ | |
$y = 3x$ | |
$y = 2x$ |
Question 6 Explanation:
Test each answer with the values in the table. Choice (B) is the only option that satisfies all the values of $x$ and $y$.
Question 7 |
If the average (arithmetic mean) of $2x$ and $4x$ is $18$, what is the value of $x$?
2 | |
3 | |
6 | |
9 |
Question 7 Explanation:
To solve this problem start with the formula for average:
$\text{Average}$ $= \frac{\text{Sum of all elements}}{\text{Number of elements}}$
$= \dfrac{(2x + 4x)}{2} = 18$
$\dfrac{(6x)}{2} = 18$
$6x = 18 * 2$
$6x = 36$
$x = 6$
$\text{Average}$ $= \frac{\text{Sum of all elements}}{\text{Number of elements}}$
$= \dfrac{(2x + 4x)}{2} = 18$
$\dfrac{(6x)}{2} = 18$
$6x = 18 * 2$
$6x = 36$
$x = 6$
Question 8 |
In a certain coffee shop, $X$ lattes were sold each hour for 6 hours on Monday, and $Y$ americanos were sold each hour for 7 hours on Monday. What expression represents the total number of lattes and americanos that were sold by the coffee shop on Monday?
$13Y + 13X$ | |
$13XY$ | |
$6Y + 7X$ | |
$6X + 7Y$ |
Question 8 Explanation:
Multiply the number of each drink sold per hour by the number of hours that drink was sold, and then added the two totals together:
$(\frac{X}{hour} * 6~hours)$ $+ (\frac{Y}{hour} * 7~hours)$ $= 6X + 7Y$
$(\frac{X}{hour} * 6~hours)$ $+ (\frac{Y}{hour} * 7~hours)$ $= 6X + 7Y$
Question 9 |
If $\dfrac{6}{z+4} = p$, and $p = 12$, what is the value of $z $?
−1.5 | |
−3.5 | |
1.5 | |
3.5 |
Question 9 Explanation:
Start by substituting $12$ for $p$ in the original equation:
$\dfrac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by $12$:
$\dfrac{6}{12} = z + 4$
Simplify the fraction:
$\dfrac{1}{2} = z + 4$
Subtract $4$:
$\dfrac{1}{2} - 4 = z$
$-3.5 = z$
$\dfrac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by $12$:
$\dfrac{6}{12} = z + 4$
Simplify the fraction:
$\dfrac{1}{2} = z + 4$
Subtract $4$:
$\dfrac{1}{2} - 4 = z$
$-3.5 = z$
Question 10 |
If a car averages 36.8 miles per gallon of gasoline, approximately how many kilometers per liter of gasoline does the car average if 1 gallon = 3.8 liters and 1 mile = 1.6 kilometers?
16 kpl | |
21 kpl | |
36 kpl | |
49 kpl |
Question 10 Explanation:
This problem is asking you to do two conversions: miles to kilometers, and gallons to liters. Both conversions can be done simultaneously to ensure correct dimensional analysis.
Set up the expression to yield the proper units:
$\frac{36.8 \text{ miles}}{1 \text{ gallon}} * \frac{1.6 \text{ km}}{1 \text{mile}} * \frac{1 \text{ gallon}}{3.8 \text{ L}}$
$= 16.25 \text{ km per liter}$
$≈ 16 \text{ km per liter}$
Set up the expression to yield the proper units:
$\frac{36.8 \text{ miles}}{1 \text{ gallon}} * \frac{1.6 \text{ km}}{1 \text{mile}} * \frac{1 \text{ gallon}}{3.8 \text{ L}}$
$= 16.25 \text{ km per liter}$
$≈ 16 \text{ km per liter}$
Question 11 |
Trains A, B and C passed through a station at different speeds. Train A’s speed was 2 times Train B’s speed and Train C’s speed was 3 times Train A’s speed. What was Train C’s speed in miles per hour, if the Train B’s speed was 9 miles per hour?
9 | |
18 | |
27 | |
54 |
Question 11 Explanation:
We can describe the situation using equations:
"Train A’s speed was 2 times Train B’s speed" ⇒ $A = 2B$
"Train C’s speed was 3 times Train A’s speed" ⇒ $C = 3A$
We know the speed of Train B is 9 miles per hour. Plugging the value of B into A, we get:
$A = 2 * 9 = 18$
Plugging the value of A into C, we get:
$C = 3A = 3*18 = 54$
"Train A’s speed was 2 times Train B’s speed" ⇒ $A = 2B$
"Train C’s speed was 3 times Train A’s speed" ⇒ $C = 3A$
We know the speed of Train B is 9 miles per hour. Plugging the value of B into A, we get:
$A = 2 * 9 = 18$
Plugging the value of A into C, we get:
$C = 3A = 3*18 = 54$
Question 12 |
In quadrilateral ABCD, what is the value of ∠ADC if ∠BAD + ∠ABC + ∠BCD = 280°?
80° | |
120° | |
160° | |
180° |
Question 12 Explanation:
For this type of Geometry question, it’s simpler to draw the figure if none is provided. Remember that just because it’s a quadrilateral, this does not necessarily mean it is a square or rectangle, so let’s draw an irregular quadrilateral.

Let’s label the angles with other letters of the alphabet so it’s easier to understand which angles we’re discussing.
The value we are looking for is angle ∠ADC, labeled as $z$. The interior angles of any quadrilateral must sum to 360°:
$w + x + y + z = 360^\circ$
$z = 360^\circ − (w + x + y)$
$280^\circ + z = 360^\circ$
$z = 80^\circ$

Let’s label the angles with other letters of the alphabet so it’s easier to understand which angles we’re discussing.
The value we are looking for is angle ∠ADC, labeled as $z$. The interior angles of any quadrilateral must sum to 360°:
$w + x + y + z = 360^\circ$
$z = 360^\circ − (w + x + y)$
$280^\circ + z = 360^\circ$
$z = 80^\circ$
Question 13 |
The weight, in pounds, of a truck with its load is given by the equation below where $w$ represents the total weight of the truck and its load, and $q$ represents the quantity of castings it is hauling. In the equation, what does the number 35,000 represent?
$w = 500q + 35,000$
The combined weight of the truck and a full load of castings | |
The weight of the truck with no load | |
The weight of each casting | |
The maximum weight of castings that the truck can haul |
Question 13 Explanation:
We are told that $w$ represents the total weight of the truck and its load, and $q$ represents the quantity of castings it is hauling. If a truck is hauling no castings, $q$ = 0. When $q$ = 0, $w$ = 500(0) + 35,000 = 35,000. In other words, the weight of the truck by itself (i.e. hauling no castings) is 35,000 lbs.
Question 14 |
Which of the following expressions is equivalent to:
$2(x − 2)^2 − 1$
$4x^2 − 16x + 15$ | |
$x^2 − 4x − 9$ | |
$2x^2 − 8x + 7$ | |
$2x^2 + 7$ |
Question 14 Explanation:
Solve this problem using the steps shown below:
$2(x − 2)^2 − 1$
$2(x − 2)(x − 2) − 1$
Use “FOIL”:
$2(x^2 + (x)(−2) + (−2)(x)$ $+~(−2)(−2)) − 1$
$2(x^2 − 2x − 2x + 4) − 1$
$2(x^2 − 4x + 4) − 1$
Distribute the 2:
$(2x^2 − 8x + 8) − 1$
$2x^2 − 8x + 7$
$2(x − 2)^2 − 1$
$2(x − 2)(x − 2) − 1$
Use “FOIL”:
$2(x^2 + (x)(−2) + (−2)(x)$ $+~(−2)(−2)) − 1$
$2(x^2 − 2x − 2x + 4) − 1$
$2(x^2 − 4x + 4) − 1$
Distribute the 2:
$(2x^2 − 8x + 8) − 1$
$2x^2 − 8x + 7$
Question 15 |
A certain item is shipped in either of two different box sizes, “large” and “small”. In yesterday’s shipments, twice as many small boxes as large boxes were used. The large box contains three times the quantity of the item that the small box contains.
If 48 boxes in total were used yesterday, and a large box holds a quantity of 9 of the item, how many items were shipped yesterday?432 | |
240 | |
336 | |
144 |
Question 15 Explanation:
Let $L$ be the number of large boxes and $S$ be the number of small boxes. Yesterday, twice as many small boxes as large boxes were used:
$S = 2L$
We are also told that yesterday 48 boxes in total were used:
$S + L = 48$
Substituting $2L$ for $S$, we have:
$2L + L = 48 → 3L = 48$ $→ L = 16$
$S = 2L → S = 2(16)$ $→ S = 32$
We used 16 Large boxes and 32 Small boxes yesterday.
A large box holds 9 items (per large box), which is three times the quantity held by a small box. This means a small box must hold 3 items (per small box).
In 16 Large boxes we would have:
$16 \text{ boxes} \ast 9 \text{ items per box}$ $= 144 \text{ items}$
In 32 Small boxes we would have:
$32 \text{ boxes} \ast 3 \text{ items per box}$ $= 96 \text{ items}$
A total of $240$ items $(144 + 96)$ were shipped yesterday.
$S = 2L$
We are also told that yesterday 48 boxes in total were used:
$S + L = 48$
Substituting $2L$ for $S$, we have:
$2L + L = 48 → 3L = 48$ $→ L = 16$
$S = 2L → S = 2(16)$ $→ S = 32$
We used 16 Large boxes and 32 Small boxes yesterday.
A large box holds 9 items (per large box), which is three times the quantity held by a small box. This means a small box must hold 3 items (per small box).
In 16 Large boxes we would have:
$16 \text{ boxes} \ast 9 \text{ items per box}$ $= 144 \text{ items}$
In 32 Small boxes we would have:
$32 \text{ boxes} \ast 3 \text{ items per box}$ $= 96 \text{ items}$
A total of $240$ items $(144 + 96)$ were shipped yesterday.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
SAT Math Practice Test 6 >>
Main Menu >>
