Below is another set of SAT Math practice questions that need to be solved without the use of a calculator. We have classified these problems as medium, but some of them are still quite challenging. This test covers the same math skills that are found on section 3 of the SAT. Continue your test prep right now with these free practice questions!
The use of a calculator is NOT permitted. Solve each problem and select the best of the answer choices provided.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A swimming pool is initially filled to a depth of 96 inches. After 2 weeks, the depth has decreased to 92½ inches. Assuming that the depth decreased at a constant rate, after how many days would the water depth have reached 93¾ inches?
3 | |
7 | |
9 | |
6 |
Question 1 Explanation:
Since the answer is asking for the number of days, we will treat 2 weeks as 14 days. In 14 days, the water level dropped from 96 to 92½ inches. That is a change of 3½ inches in 14 days; this would be the same as 7 inches in 28 days (doubling the numerator and denominator), which can be reduced to 1 inch in 4 days; or ¼ inch for each day.
We are asked how many days it would take at the rate of ¼ inch per day for the depth to go from 96 to 93¾ inches, a change of 2¼ inches. We can think of 2¼ inches as 1 inch (4 days) + 1 inch (4 days) + ¼ inch (1 day), a total of 9 days.
The above approach is one such “no-calculator” approach to solving the following:
$\dfrac{3\frac{1}{2} \text{ inches}}{14 \text{ days}} = \dfrac{2\frac{1}{4} \text{ inches}}{x \text{ days}}$
We are asked how many days it would take at the rate of ¼ inch per day for the depth to go from 96 to 93¾ inches, a change of 2¼ inches. We can think of 2¼ inches as 1 inch (4 days) + 1 inch (4 days) + ¼ inch (1 day), a total of 9 days.
The above approach is one such “no-calculator” approach to solving the following:
$\dfrac{3\frac{1}{2} \text{ inches}}{14 \text{ days}} = \dfrac{2\frac{1}{4} \text{ inches}}{x \text{ days}}$
Question 2 |
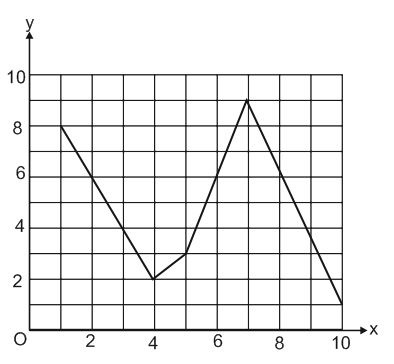
The graph of $y = f(x)$ is shown above. If $f(3) = k$, which of the following could be the value of $f(k)$?
2 | |
3.5 | |
4 | |
4.5 |
Question 2 Explanation:
We know that $f(3) = k$. Using the graph, we can see that $f(3) = 4$.
Plugging in the value of $k = 4$, we get: $f(k) = f(4) = 2$
Plugging in the value of $k = 4$, we get: $f(k) = f(4) = 2$
Question 3 |
$2x + 4y = 16$
$3x − 6y = 12$ If ($x, y$) is a solution to the system of equations above, what is the value of $x + y$?5 | |
6 | |
7 | |
8 |
Question 3 Explanation:
Start by simplifying each equation. Do the terms have any common factors? Notice that 2, 4, and 16 from the first equation can all be divided by 2:
$x + 2y = 8$
Likewise, we can divide the second equation by 3:
$x − 2y = 4$
Using the method of Elimination/Combination, we can cancel out the 2$y$ term if we add both equations together:
$~~~~~x + 2y = 8$
$\underline{+ (x − 2y = 4)}$
$~~~~2x~~~~~~~=12$
$x = 6$
Plugging $x$ = 6 back into either equation:
$(6) + 2y = 8$
Solving for $y$, we get:
$y = 1$
The question is asking for $x + y$, so:
$x + y = (6) + (1) = 7$
$x + 2y = 8$
Likewise, we can divide the second equation by 3:
$x − 2y = 4$
Using the method of Elimination/Combination, we can cancel out the 2$y$ term if we add both equations together:
$~~~~~x + 2y = 8$
$\underline{+ (x − 2y = 4)}$
$~~~~2x~~~~~~~=12$
$x = 6$
Plugging $x$ = 6 back into either equation:
$(6) + 2y = 8$
Solving for $y$, we get:
$y = 1$
The question is asking for $x + y$, so:
$x + y = (6) + (1) = 7$
Question 4 |
If $\dfrac{1}{y} - \dfrac{1}{y + 1} = \dfrac{1}{y + 3}$, then $y$ could be
$2$ | |
$0$ | |
$-2$ | |
$\sqrt{3}$ |
Question 4 Explanation:
In this case, multiplying each term by the least common multiple (LCM) of the denominators will best clarify the problem:
$\dfrac{y(y+1)(y+3)}{y} -$ $\dfrac{y(y+1)(y+3)}{y+1} =$ $\dfrac{y(y+3)(y+1)}{y+3}$
The denominators will all cancel out, and the remaining numerators can be distributed:
$(y+1)(y+3) - (y)(y+3)$ = $(y)(y+1)$
$y^2 + 3y + 1y + 3 - y^2 - 3y$ = $y^2 + y$
Combine like terms:
$3+y = y^2 + y$
Subtract $y$ from both sides:
$3 = y^2$
$y = ±\sqrt{3}$
An alternate approach is to work backwards and try each of the answer choices.
$\dfrac{y(y+1)(y+3)}{y} -$ $\dfrac{y(y+1)(y+3)}{y+1} =$ $\dfrac{y(y+3)(y+1)}{y+3}$
The denominators will all cancel out, and the remaining numerators can be distributed:
$(y+1)(y+3) - (y)(y+3)$ = $(y)(y+1)$
$y^2 + 3y + 1y + 3 - y^2 - 3y$ = $y^2 + y$
Combine like terms:
$3+y = y^2 + y$
Subtract $y$ from both sides:
$3 = y^2$
$y = ±\sqrt{3}$
An alternate approach is to work backwards and try each of the answer choices.
Question 5 |
If $(x)^{-1} = -\dfrac{1}{2}$ then $(x)^{-2}$ equals which of the following?
$-4$ | |
$-1$ | |
$-\dfrac{1}{4}$ | |
$\dfrac{1}{4}$ |
Question 5 Explanation:
A negative exponent is another way of writing a fraction:
$(x)$$-1$ = $\dfrac{1}{x}$
If $\dfrac{1}{x} = -\dfrac{1}{2}$, then $x = -2$
$(x)^{-2} = (-2)^{-2} = \dfrac{1}{4}$
$(x)$$-1$ = $\dfrac{1}{x}$
If $\dfrac{1}{x} = -\dfrac{1}{2}$, then $x = -2$
$(x)^{-2} = (-2)^{-2} = \dfrac{1}{4}$
Question 6 |
In the coordinate plane, line $m$ passes through the origin and has a slope of $3$. If points $(6, y)$ and $(x, 12)$ are on line $m$, then $y − x = \; ?$
14 | |
18 | |
22 | |
26 |
Question 6 Explanation:
The standard equation of a line is $y = mx + b$, where $m$ is the slope, $b$ is the y-intercept, and ($x, y$) represent any coordinate pair on the line. Let’s fill in the equation of line $m$ based on what we know:
$y = 3x + b$
Since the line passes through the origin (0, 0), we know the y-intercept is 0:
$y = 3x$
To find what $y$ is when $x$ = 6, plug in $x$ = 6:
(6, 18) is a point on the line, and $y$ = 18
To find $y$, plug in 12 for $y$:
$12 = 3x$
$4 = x$
(4, 12) is a point on the line, and $x$ = 4
$y − x = 18 − 4 = 14$
$y = 3x + b$
Since the line passes through the origin (0, 0), we know the y-intercept is 0:
$y = 3x$
To find what $y$ is when $x$ = 6, plug in $x$ = 6:
(6, 18) is a point on the line, and $y$ = 18
To find $y$, plug in 12 for $y$:
$12 = 3x$
$4 = x$
(4, 12) is a point on the line, and $x$ = 4
$y − x = 18 − 4 = 14$
Question 7 |
If the function $f(x)$ is defined for all real numbers by the following equation: $f(x) = \dfrac{x^2 + 2}{2}$
Then $f(f(2)) = $
1.5 | |
3.0 | |
5.5 | |
7.0 |
Question 7 Explanation:
To solve this function question, start by substituting 2 for $x$:
$f(2) = \dfrac{2^2+2}{2}$
$f(2) = \dfrac{4+2}{2}$
$f(2) = \dfrac{6}{2}$
$f(2) = 3$
But we can't stop there! Notice the question asks for the value of $f(f(2))$
$f(2)$ = $3$, so $f(f(2))$ = $f(3)$
Substitute 3 for $x$ in the function to get the the final answer:
$f(3) = \dfrac{3^2+2}{2}$
$f(3) = \dfrac{9+2}{2}$
$f(3) = \dfrac{11}{2}$
$f(3)$ = $5.5$
$f(2) = \dfrac{2^2+2}{2}$
$f(2) = \dfrac{4+2}{2}$
$f(2) = \dfrac{6}{2}$
$f(2) = 3$
But we can't stop there! Notice the question asks for the value of $f(f(2))$
$f(2)$ = $3$, so $f(f(2))$ = $f(3)$
Substitute 3 for $x$ in the function to get the the final answer:
$f(3) = \dfrac{3^2+2}{2}$
$f(3) = \dfrac{9+2}{2}$
$f(3) = \dfrac{11}{2}$
$f(3)$ = $5.5$
Question 8 |
A delivery cart went from Candleford to Lark Rise and back at an average speed of $\frac{2}{3}$ miles per hour. If the distance from Candleford to Lark Rise is 1 mile, and the trip back took half as much time as the trip there, what was the average speed of the delivery cart on the way to Lark Rise?
$\dfrac{1}{3}$ | |
$\dfrac{1}{2}$ | |
$\dfrac{3}{4}$ | |
$\dfrac{2}{3}$ |
Question 8 Explanation:
It’s important to first understand what this question is asking. “On the way to Lark Rise” means the way there. The question is asking the average speed for a portion of the total trip. To find it, we’ll need to know the distance for that part of the trip and the time spent on that part of the trip.
If the average speed of the entire journey was $\frac{2}{3}$ miles per hour, then for every 3 hours, 2 miles were traveled. Since the total distance was 2 miles, the total time must have been 3 hours.
If the way back took half as much time as the way there, then for every 3 hours, 2 hours was spent on the way there, and 1 hour was spent on the way back.
Average Speed = $\frac{\text{Distance}}{\text{Time}} = \frac{1 \text{ mile}}{2 \text{ hours}}$
The average speed for the way to Lark Rise was $\frac{1}{2}$ mph.
If the average speed of the entire journey was $\frac{2}{3}$ miles per hour, then for every 3 hours, 2 miles were traveled. Since the total distance was 2 miles, the total time must have been 3 hours.
If the way back took half as much time as the way there, then for every 3 hours, 2 hours was spent on the way there, and 1 hour was spent on the way back.
Average Speed = $\frac{\text{Distance}}{\text{Time}} = \frac{1 \text{ mile}}{2 \text{ hours}}$
The average speed for the way to Lark Rise was $\frac{1}{2}$ mph.
Question 9 |
If $a = \frac{-1}{b}$ and $c = \frac{1}{d}$ for integers $a, b, c$ and $d$, in which of the following ranges does the product $abcd$ fall?
$−4 < abcd < −2$ | |
$−2 < abcd < 0$ | |
$0 < abcd < 2$ | |
$2 < abcd < 4$ |
Question 9 Explanation:
The expression $abcd$ can be rewritten as:
$abcd = \left(\dfrac{-1}{b}\right)b * \left(\dfrac{1}{d}\right)d$
$= (-1)(1) = -1$
Only choice (B) correctly places $abcd$ in the range $−2 < −1 < 0$.
$abcd = \left(\dfrac{-1}{b}\right)b * \left(\dfrac{1}{d}\right)d$
$= (-1)(1) = -1$
Only choice (B) correctly places $abcd$ in the range $−2 < −1 < 0$.
Question 10 |
ΔABC is an equilateral triangle. AB = AD. What is the value of x?
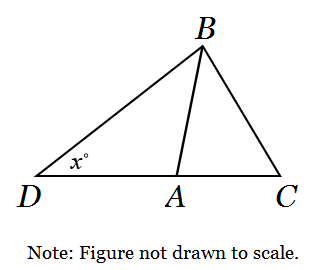
45 | |
20 | |
60 | |
30 |
Question 10 Explanation:
Since ΔABC is an equilateral triangle, each of its interior angles must be 60°.
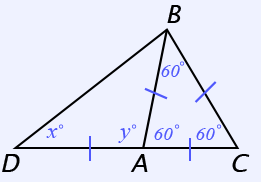
∠BAC = 60°
∠BAD + ∠BAC = 180°
∠BAD + 60° = 180°
∠BAD = 120°
y = 120°
Since AB = AD, ΔABD is isosceles. This means its base angles, ∠ABD and ∠ADB, are congruent; both equal x°.
The interior angles of any triangle sum to 180°:
∠ADB + ∠ABD + ∠BAD = 180°
x + x + y = 180
x + x + 120 = 180
2x = 60
x = 30°

∠BAC = 60°
∠BAD + ∠BAC = 180°
∠BAD + 60° = 180°
∠BAD = 120°
y = 120°
Since AB = AD, ΔABD is isosceles. This means its base angles, ∠ABD and ∠ADB, are congruent; both equal x°.
The interior angles of any triangle sum to 180°:
∠ADB + ∠ABD + ∠BAD = 180°
x + x + y = 180
x + x + 120 = 180
2x = 60
x = 30°
Question 11 |
$a = 3 - i$ where $i = \sqrt{-1}$
What is the value of $a^2$?
$6 − 2i$ | |
$8$ | |
$8 - 6i$ | |
$9 + i$ |
Question 11 Explanation:
This problem can be solved as shown below.
We are given: $a = 3 - i$
$a^2 = (3 - i)(3 - i)$
We need to “FOIL":
$(3)(3) + (3)(-i) + (-i)(3)$ $+ (-i)(-i)$
$9 - 3i - 3i + i^2$
$9 - 6i + i^2$
Since $i = \sqrt{-1}, ~i^2 = -1$
$9 - 6i - 1$
$8 - 6i$
We are given: $a = 3 - i$
$a^2 = (3 - i)(3 - i)$
We need to “FOIL":
$(3)(3) + (3)(-i) + (-i)(3)$ $+ (-i)(-i)$
$9 - 3i - 3i + i^2$
$9 - 6i + i^2$
Since $i = \sqrt{-1}, ~i^2 = -1$
$9 - 6i - 1$
$8 - 6i$
Question 12 |
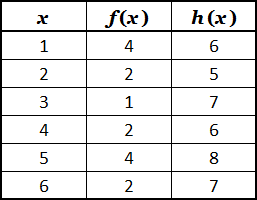
The table above shows values of the functions $f$ and $h$. For which value of $x$ is $h(f(x)) = 2x$?
1 | |
3 | |
2 | |
4 |
Question 12 Explanation:
It is easiest to try each answer to see which works.
Let’s start with $x = 1$:
If $x = 1$ then, from the table, $f(1) = 4$
$h(f(x)) = h(f(1)) = h(4)$, since $f(1) = 4$
From the table, $h(4) = 6$
$h(f(1)) = 6; \, 2x = 2(1) = 2$
This answer does not work.
Let’s try $x = 3$:
If $x = 3$ then, from the table, $f(3) = 1$
$h(f(x)) = h(f(3)) = h(1)$, since $f(3) = 1$
From the table, $h(1) = 6$
$h(f(3)) = 6; \, 2x = 2(3) = 6$
This answer works.
Let’s start with $x = 1$:
If $x = 1$ then, from the table, $f(1) = 4$
$h(f(x)) = h(f(1)) = h(4)$, since $f(1) = 4$
From the table, $h(4) = 6$
$h(f(1)) = 6; \, 2x = 2(1) = 2$
This answer does not work.
Let’s try $x = 3$:
If $x = 3$ then, from the table, $f(3) = 1$
$h(f(x)) = h(f(3)) = h(1)$, since $f(3) = 1$
From the table, $h(1) = 6$
$h(f(3)) = 6; \, 2x = 2(3) = 6$
This answer works.
Question 13 |
If a, b, c are integers, let a▲(b,c) be defined to be true only if b ≤ a ≤ c. If −3▲(b,0) is true, which of these could be a possible value of b?
I. −3
II. 5
III. −5
I only | |
I and II | |
I and III | |
All are correct |
Question 13 Explanation:
If $-3▲(b,0)$ is true, then $b ≤ -3 ≤ 0$
Thus, $b = -3$ or $b = -5$
Thus, $b = -3$ or $b = -5$
Question 14 |
Farmer Hank is buying cows and goats. Cows cost \$150 per month to feed. Goats cost \$50 per month to feed. The land required for the animals is 1 acre for each cow and 1 acre for every 4 goats. The most he can spend on feeding these animals is \$2500 per month. The maximum amount of land he can provide to the cows and goats is 14 acres. Hank wants the ratio of goats to cows to exceed 2 to 1.
Which set of inequalities best represents the set of conditions described if c is the number of cows and g is the number of goats?
150c + 50g ≤ 2500
1c + 4g ≤ 14 g > 2c | |
200(c + g) ≤ 2500
1c + 4g ≤ 14 2g > c | |
150c + 50g ≤ 2500
1c + $\frac{1}{4}$g ≤ 14 2g > c | |
150c + 50g ≤ 2500
1c + $\frac{1}{4}$g ≤ 14 g > 2c |
Question 14 Explanation:
The total cost of feeding c cows and g goats is represented by 150c + 50g. The most he can spend is $2500 per month means “less than or equal to.” 150c + 50g ≤ 2500 correctly represents this condition.
If we had 2 cows and 12 goats we would need 1 acre for each cow and 1 acre for each set of 4 goats. In total we would need 2 acres for the cows and 3 acres for the 12 goats, or 5 acres all-together. 1c + $\frac{1}{4}$g is the only choice that gives 5 acres when we plug in c = 2 and g = 12. 1c + $\frac{1}{4}$g ≤ 14 correctly represents this condition.
Finally, we are told that Hank wants the ratio of goats to cows to exceed 2 to 1. That means he wants more than 2 goats for every 1 cow. For example, if he has 3 goats and 1 cow, he would be happy. g > 2c correctly represents this condition.
If we had 2 cows and 12 goats we would need 1 acre for each cow and 1 acre for each set of 4 goats. In total we would need 2 acres for the cows and 3 acres for the 12 goats, or 5 acres all-together. 1c + $\frac{1}{4}$g is the only choice that gives 5 acres when we plug in c = 2 and g = 12. 1c + $\frac{1}{4}$g ≤ 14 correctly represents this condition.
Finally, we are told that Hank wants the ratio of goats to cows to exceed 2 to 1. That means he wants more than 2 goats for every 1 cow. For example, if he has 3 goats and 1 cow, he would be happy. g > 2c correctly represents this condition.
Question 15 |
Sam is paid by the hour and receives 1.5 times her hourly pay for each hour she works in excess of 40 hours in a given week. She saves 10% of the money she earns and has been averaging 46 hours of work each week.
Assuming she continues to save 10% of her earnings and continues to work 46 hours per week, how much more per hour would Sam’s base pay need to increase for her to increase her yearly savings by $468?$1.84 per hour | |
$2.16 per hour | |
$1.96 per hour | |
$2.25 per hour |
Question 15 Explanation:
First, let's determine how much Sam currently saves each week.
Let p be per current hourly pay. Her hourly pay is increased to 1.5p for the 6 hours she works in excess of 40 hours:
Weekly Earnings = 40p + 6(1.5p)
Weekly Earnings = 40p + 9p
Weekly Earnings = 49p
She saves 10% of her Weekly Earnings:
Weekly Savings = 0.10(49p)
Weekly Savings = 4.9p
Next let's determine how much she would save if her pay increases by x:
Future Weekly Earnings = 40(p + x) + 6(1.5(p + x))
Future Weekly Earnings = 40(p + x) + 9(p + x)
Future Weekly Earnings = 49(p + x)
She still will save 10% of her earnings:
Future Weekly Savings = 0.10(49(p + x))
Future Weekly Savings = 4.9(p + x)
Her savings have increased from 4.9p to 4.9(p + x).
This is an increase of 4.9x \$/wk
(since 4.9(p + x) − 4.9p = 4.9x)
Finally, we can determine what x needs to be:
(4.9x \$/wk)(52 wk/yr) = 468 \$/yr
Solving for x:
x = \$1.84
Let p be per current hourly pay. Her hourly pay is increased to 1.5p for the 6 hours she works in excess of 40 hours:
Weekly Earnings = 40p + 6(1.5p)
Weekly Earnings = 40p + 9p
Weekly Earnings = 49p
She saves 10% of her Weekly Earnings:
Weekly Savings = 0.10(49p)
Weekly Savings = 4.9p
Next let's determine how much she would save if her pay increases by x:
Future Weekly Earnings = 40(p + x) + 6(1.5(p + x))
Future Weekly Earnings = 40(p + x) + 9(p + x)
Future Weekly Earnings = 49(p + x)
She still will save 10% of her earnings:
Future Weekly Savings = 0.10(49(p + x))
Future Weekly Savings = 4.9(p + x)
Her savings have increased from 4.9p to 4.9(p + x).
This is an increase of 4.9x \$/wk
(since 4.9(p + x) − 4.9p = 4.9x)
Finally, we can determine what x needs to be:
(4.9x \$/wk)(52 wk/yr) = 468 \$/yr
Solving for x:
x = \$1.84
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
Next Practice Test:
SAT Math Practice Test 7 >>
Main Menu >>
