SAT Math No Calculator practice tests.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
In a certain coffee shop, $X$ lattes were sold each hour for 6 hours on Monday, and $Y$ americanos were sold each hour for 7 hours on Monday. What expression represents the total number of lattes and americanos that were sold by the coffee
shop on Monday?
$13Y + 13X$ | |
$13XY$ | |
$6Y + 7X$ | |
$6X + 7Y$ |
Question 1 Explanation:
The correct answer is (D).
$(\dfrac{X}{hour} * 6~hours) + (\dfrac{Y}{hour} * 7~hours) = 6X + 7Y$
Notice that we multiplied the number of each drink by the number of hours that drink was sold, and then added the two totals together: $(6*X) + (7*Y).$
This matches the expression in answer choice (D).
Alternatively, this solution can be verified by testing values. Let’s say $X = 2$ and $Y = 3$. If 2 lattes were sold each hour for 6 hours, then $2 * 6 = 12$ lattes total were sold.
Similarly, if 3 americanos were sold each hour for 7 hours, then $3 * 7 = 21$ americanos were sold.
The total number of lattes and americanos would therefore be $12 + 21 = 33$. Plug in $X = 2$ and $Y = 3$ into the answer choices. The one that yields 33 is correct.
$(\dfrac{X}{hour} * 6~hours) + (\dfrac{Y}{hour} * 7~hours) = 6X + 7Y$
Notice that we multiplied the number of each drink by the number of hours that drink was sold, and then added the two totals together: $(6*X) + (7*Y).$
This matches the expression in answer choice (D).
Alternatively, this solution can be verified by testing values. Let’s say $X = 2$ and $Y = 3$. If 2 lattes were sold each hour for 6 hours, then $2 * 6 = 12$ lattes total were sold.
Similarly, if 3 americanos were sold each hour for 7 hours, then $3 * 7 = 21$ americanos were sold.
The total number of lattes and americanos would therefore be $12 + 21 = 33$. Plug in $X = 2$ and $Y = 3$ into the answer choices. The one that yields 33 is correct.
Question 2 |
If $\dfrac{6}{z+4} = p$, and $p = 12$, what is the value of $z $?
−1.5 | |
−3.5 | |
1.5 | |
3.5 |
Question 2 Explanation:
The correct answer is (B).
Start by substituting 12 for p in the original equation:
$\dfrac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by 12:
$\dfrac{6}{12} = z + 4$
Simplify the fraction:
$\dfrac{1}{2} = z + 4$
Subtract 4:
$\dfrac{1}{2} - 4 = z$
$-3.5 = z$
Start by substituting 12 for p in the original equation:
$\dfrac{6}{z + 4} = 12$
Because the unknown is in the denominator, and the equation represents a simple proportion, we can simplify the problem by cross multiplying and then dividing:
$6 = 12(z + 4)$
Divide both sides by 12:
$\dfrac{6}{12} = z + 4$
Simplify the fraction:
$\dfrac{1}{2} = z + 4$
Subtract 4:
$\dfrac{1}{2} - 4 = z$
$-3.5 = z$
Question 3 |
If the function ƒ(x) is defined for all real numbers by the following equation: $f(x) = \dfrac{x^2 + 2}{2}$
Then $f(f(2)) = $
1.5 | |
3.0 | |
5.5 | |
7.0 |
Question 3 Explanation:
The correct answer is (C).
To solve this function question, start by substituting $2$ for $x$:
$f(2) = \dfrac{2^2+2}{2}$
$f(2) = \dfrac{4+2}{2}$
$f(2) = \dfrac{6}{2}$
$f(2) = 3$
But we can't stop there! Notice the question asks for the value of $f(f(2))$
$f(2)$ = $3$, so $f(f(2))$ = $f(3)$
Substitute $3$ for $x$ in the function to get the the final answer:
$f(3) = \dfrac{3^2+2}{2}$
$f(3) = \dfrac{9+2}{2}$
$f(3) = \dfrac{11}{2}$
$f(3)$ = $5.5$
To solve this function question, start by substituting $2$ for $x$:
$f(2) = \dfrac{2^2+2}{2}$
$f(2) = \dfrac{4+2}{2}$
$f(2) = \dfrac{6}{2}$
$f(2) = 3$
But we can't stop there! Notice the question asks for the value of $f(f(2))$
$f(2)$ = $3$, so $f(f(2))$ = $f(3)$
Substitute $3$ for $x$ in the function to get the the final answer:
$f(3) = \dfrac{3^2+2}{2}$
$f(3) = \dfrac{9+2}{2}$
$f(3) = \dfrac{11}{2}$
$f(3)$ = $5.5$
Question 4 |
If a car averages 36.8 miles per gallon of gasoline, approximately how many kilometers per liter of gasoline does the car average if 1 gallon = 3.8 liters and 1 mile = 1.6 kilometers?
16 kpl | |
21 kpl | |
36 kpl | |
49 kpl |
Question 4 Explanation:
The correct answer is (A).
This problem is asking you to do two conversions: miles to kilometers, and gallons to liters. Both conversions can be done simultaneously to ensure correct dimensional analysis.
Set up the expression to yield the proper units:
$\dfrac{36.8~miles}{1~gallon} * \dfrac{1.6~km}{1~mile} * \dfrac{1~gallon}{3.8~L} = 15.49~km~per~liter$
$ ≈ 16~kpl$
This problem is asking you to do two conversions: miles to kilometers, and gallons to liters. Both conversions can be done simultaneously to ensure correct dimensional analysis.
Set up the expression to yield the proper units:
$\dfrac{36.8~miles}{1~gallon} * \dfrac{1.6~km}{1~mile} * \dfrac{1~gallon}{3.8~L} = 15.49~km~per~liter$
$ ≈ 16~kpl$
Question 5 |
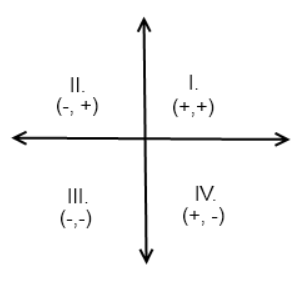 If the product of x and y does not equal zero, which of the following could be true based on the figure above?
If the product of x and y does not equal zero, which of the following could be true based on the figure above?
I. (−x, y) lies above the x-axis and to the right of the y-axis.
II. (x, −y) lies below the x-axis and to the left of the y-axis.
III. (x, y) lies on the x-axis to the right of the y-axis.
I only | |
II only | |
I and II only | |
II and III |
Question 5 Explanation:
The correct answer is (C).
For choice I, if (−x, y) lies above the x-axis and to the right of the y-axis (in the first quadrant), then x must equal a negative number, since all x-values to the right of the y-axis are positive. The only way -x = positive is if x = negative. So, y must be positive since it is above the x-axis. This is possible.
For choice II, if (x, −y) is in the third quadrant, then x = negative, and -y = negative. This is only true if x = negative and y = positive. This is also possible.
For choice III, if a point lies on the x-axis, then its value is 0, that would make the product of x and y zero, which contradicts the given information.
Given the constraints of the problem, only the first two Roman numerals are possible answer choices.
For choice I, if (−x, y) lies above the x-axis and to the right of the y-axis (in the first quadrant), then x must equal a negative number, since all x-values to the right of the y-axis are positive. The only way -x = positive is if x = negative. So, y must be positive since it is above the x-axis. This is possible.
For choice II, if (x, −y) is in the third quadrant, then x = negative, and -y = negative. This is only true if x = negative and y = positive. This is also possible.
For choice III, if a point lies on the x-axis, then its value is 0, that would make the product of x and y zero, which contradicts the given information.
Given the constraints of the problem, only the first two Roman numerals are possible answer choices.
Question 6 |
2x + 4y = 16
3x − 6y = 12
If (x,y) is a solution to the system of equations above, what is the value of x + y?
3x − 6y = 12
If (x,y) is a solution to the system of equations above, what is the value of x + y?
5 | |
6 | |
7 | |
8 |
Question 6 Explanation:
The correct answer is (C).
Start by simplifying each equation. Do the terms have any common factors? Notice that 2, 4, and 16 from the first equation can all be divided by 2:
$x + 2y = 8$
Likewise, we can divide the second equation by 3:
$x − 2y = 4$
Using the method of Elimination/Combination, we can cancel out the $2y$ term if we add both equations together:
$x + 2y = 8$
$+ (x − 2y = 4)$
——————-
$2x = 12$
$x = 6$
Plugging $x = 6$ back into either equation:
$(6) + 2y = 8$
Solving for y, we get:
$y = 1$.
The question is asking for $x + y$, so:
$x + y = (6) + (1) = 7$
Start by simplifying each equation. Do the terms have any common factors? Notice that 2, 4, and 16 from the first equation can all be divided by 2:
$x + 2y = 8$
Likewise, we can divide the second equation by 3:
$x − 2y = 4$
Using the method of Elimination/Combination, we can cancel out the $2y$ term if we add both equations together:
$x + 2y = 8$
$+ (x − 2y = 4)$
——————-
$2x = 12$
$x = 6$
Plugging $x = 6$ back into either equation:
$(6) + 2y = 8$
Solving for y, we get:
$y = 1$.
The question is asking for $x + y$, so:
$x + y = (6) + (1) = 7$
Question 7 |
If Eric was 22 years old x years ago and Shelley will be 24 years old in y years, what was the average of their ages 4 years ago?
$\dfrac{x + y}{2}$ | |
$\dfrac{y + 38}{3}$ | |
$\dfrac{x - y + 28}{4}$ | |
$\dfrac{x - y + 38}{2}$ |
Question 7 Explanation:
The correct answer is (D).
The problem asks for the average of the ages of 2 people. Thus, the divisor will be 2, and answer choices (B) and (C) can be eliminated. That leaves us with just (A) and (D).
Let's start off by converting the problem into mathematical expressions.
If Eric was 22 years old x years ago, then he is currently $22 + x$ years old.
If Shelley will be 24 years old in y years, then she is currently $24 - y$ years old.
(If these expressions seem confusing to you, try plugging in some numbers to convince yourself that they hold true.)
This means, that 4 years ago, Eric was $x + 22 - 4 = x + 18$ years old.
Likewise, 4 years ago, Shelley was $24 - y - 4 = 20 - y$ years old.
Taking the average of these two ages, we get:
$\dfrac{x + 18 + 20 - y}{2} = \dfrac{x - y + 38}{2}$
The problem asks for the average of the ages of 2 people. Thus, the divisor will be 2, and answer choices (B) and (C) can be eliminated. That leaves us with just (A) and (D).
Let's start off by converting the problem into mathematical expressions.
If Eric was 22 years old x years ago, then he is currently $22 + x$ years old.
If Shelley will be 24 years old in y years, then she is currently $24 - y$ years old.
(If these expressions seem confusing to you, try plugging in some numbers to convince yourself that they hold true.)
This means, that 4 years ago, Eric was $x + 22 - 4 = x + 18$ years old.
Likewise, 4 years ago, Shelley was $24 - y - 4 = 20 - y$ years old.
Taking the average of these two ages, we get:
$\dfrac{x + 18 + 20 - y}{2} = \dfrac{x - y + 38}{2}$
Question 8 |
In the coordinate plane, line m passes through the origin and has a slope of 3. If points (6,y) and (x,12) are on line m, then y − x = ?
14 | |
18 | |
22 | |
26 |
Question 8 Explanation:
The correct answer is (A).
The standard equation of a line is y = mx + b, where m is the slope, b is the y-intercept, and (x, y) represent any coordinate pair on the line. Let’s fill in the equation of line m based on what we know:
$y = 3x + b$
Since the line passes through the origin $(0,0)$, we know the y-intercept is 0:
$y = 3x$
To find what y is when $x = 6$, plug in $x = 6$.
$(6,18)$ is a point on the line, and $y = 18$.
To find y, plug in 12 for y:
$12 = 3x$
$4 = x$
$(4, 12)$ is a point on the line, and $x = 4$.
$y − x = 18 − 4 = 14$
The standard equation of a line is y = mx + b, where m is the slope, b is the y-intercept, and (x, y) represent any coordinate pair on the line. Let’s fill in the equation of line m based on what we know:
$y = 3x + b$
Since the line passes through the origin $(0,0)$, we know the y-intercept is 0:
$y = 3x$
To find what y is when $x = 6$, plug in $x = 6$.
$(6,18)$ is a point on the line, and $y = 18$.
To find y, plug in 12 for y:
$12 = 3x$
$4 = x$
$(4, 12)$ is a point on the line, and $x = 4$.
$y − x = 18 − 4 = 14$
Question 9 |
If $\dfrac{1}{y} - \dfrac{1}{y + 1}$ = $\dfrac{1}{y + 3}$, then $y$ could be
2 | |
0 | |
-2 | |
√3 |
Question 9 Explanation:
The correct answer is (D).
In this case, multiplying each term by the least common multiple (LCM) of the denominators will best clarify the problem:
$\dfrac{y(y+1)(y+3)}{y} - \dfrac{y(y+1)(y+3)}{y+1} = \dfrac{y(y+3)(y+1)}{y+3}$
The denominators will all cancel out, and the remaining numerators can be distributed:
$(y+1)(y+3) - (y)(y+3) = (y)(y+1)$
$y^2 + 3y + 3 - y^2 - 3y = y^2 + y$
Combine like terms:
$3+y = y^2 + y$
Subtract y from both sides:
$3 = y^2$
$y = √3$
An alternate approach is to work backwards and try each of the answer choices. However, that is a very time-consuming method, and is better suited only for verifying your answer.
In this case, multiplying each term by the least common multiple (LCM) of the denominators will best clarify the problem:
$\dfrac{y(y+1)(y+3)}{y} - \dfrac{y(y+1)(y+3)}{y+1} = \dfrac{y(y+3)(y+1)}{y+3}$
The denominators will all cancel out, and the remaining numerators can be distributed:
$(y+1)(y+3) - (y)(y+3) = (y)(y+1)$
$y^2 + 3y + 3 - y^2 - 3y = y^2 + y$
Combine like terms:
$3+y = y^2 + y$
Subtract y from both sides:
$3 = y^2$
$y = √3$
An alternate approach is to work backwards and try each of the answer choices. However, that is a very time-consuming method, and is better suited only for verifying your answer.
Question 10 |
If a = $\dfrac{-1}{b}$ and c = $\dfrac{1}{d}$ for integers a, b, c and d, in which of the following ranges does the product abcd fall?
−4 < abcd < -2 | |
−2 < abcd < 0 | |
0 < abcd < 2 | |
2 < abcd < 4 |
Question 10 Explanation:
The correct answer is (B).
The expression abcd can be rewritten as:
abcd = $b(\dfrac{-1}{b})*(\dfrac{1}{d})d = (-1)(1) = -1$
Only answer choice (B) correctly places abcd in the range −2 < −1 < 0.
The expression abcd can be rewritten as:
abcd = $b(\dfrac{-1}{b})*(\dfrac{1}{d})d = (-1)(1) = -1$
Only answer choice (B) correctly places abcd in the range −2 < −1 < 0.
Question 11 |
The average of several test scores is 80. One make-up exam was given. Included with the other scores, the new average was 84. If the score on the make-up exam was 92, how many total exams were given?
2 | |
3 | |
4 | |
5 |
Question 11 Explanation:
The correct answer is (B).
Recall that average is calculated by adding a group of numbers and then dividing by the count of those numbers. Plugging in what we’re given to the formula for average:
$80 = \dfrac{Sum}{x}$
$80x = Sum$
$84 = \dfrac{(Sum~+~Makeup~Score)}{(x+1)}$
Multiplying both sides by $x + 1$:
$84x + 84 = Sum~+~ Makeup~Score$
Let’s substitute 80x for Sum:
$84x + 84 = 80x + Makeup~Score$
$4x + 84 = Makeup~Score$
We are told that the makeup score was 92:
$4x + 84 = 92$
$4x = 8$
$x = 2$
The question asks for the total number of exams, which is $x+1 = 3$
Recall that average is calculated by adding a group of numbers and then dividing by the count of those numbers. Plugging in what we’re given to the formula for average:
$80 = \dfrac{Sum}{x}$
$80x = Sum$
$84 = \dfrac{(Sum~+~Makeup~Score)}{(x+1)}$
Multiplying both sides by $x + 1$:
$84x + 84 = Sum~+~ Makeup~Score$
Let’s substitute 80x for Sum:
$84x + 84 = 80x + Makeup~Score$
$4x + 84 = Makeup~Score$
We are told that the makeup score was 92:
$4x + 84 = 92$
$4x = 8$
$x = 2$
The question asks for the total number of exams, which is $x+1 = 3$
Question 12 |
If (x)-1 = $\dfrac{-1}{2}$ then (x)-2 equals which of the following?
-4 | |
-1 | |
$\dfrac{-1}{4}$ | |
$\dfrac{1}{4}$ |
Question 12 Explanation:
The correct answer is (D).
A negative exponent is another way of writing a fraction:
$(x)$$-1$ = $\dfrac{1}{x}$
If $\dfrac{1}{x} = -\dfrac{1}{2}$, then $x = -2$
$(x)$$-2$ = $(-2)$$-2$ = $\dfrac{1}{4}$
A negative exponent is another way of writing a fraction:
$(x)$$-1$ = $\dfrac{1}{x}$
If $\dfrac{1}{x} = -\dfrac{1}{2}$, then $x = -2$
$(x)$$-2$ = $(-2)$$-2$ = $\dfrac{1}{4}$
Question 13 |
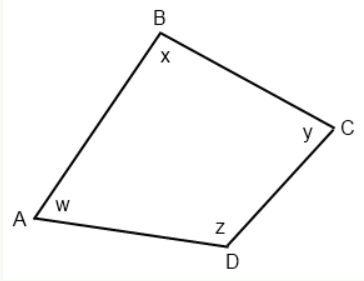
In quadrilateral ABCD, what is the value of ∠ADC∠if ∠BAD + ∠ABC + ∠BCD = 280°?

80° | |
120° | |
160° | |
180° |
Question 13 Explanation:
The correct answer is (A).
For this type of Geometry question, it’s simpler to draw the figure if none is provided. Remember that just because it’s a quadrilateral, this does not necessarily mean it is a square or rectangle, so let’s draw an irregular quadrilateral.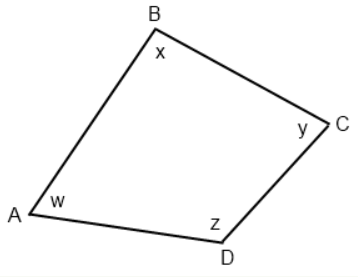
The value we are looking for is angle ∠ADC, here labeled as z. The interior angles of any quadrilateral must sum to 360°:
$W + X + Y + Z = 360°$
$Z = 360° − (W + X + Y)$
$280° + Z = 360° $ so $Z = 80°.$
For this type of Geometry question, it’s simpler to draw the figure if none is provided. Remember that just because it’s a quadrilateral, this does not necessarily mean it is a square or rectangle, so let’s draw an irregular quadrilateral.

Let’s label the angles with other letters of the alphabet so it’s easier to understand which angles we’re discussing.
The value we are looking for is angle ∠ADC, here labeled as z. The interior angles of any quadrilateral must sum to 360°:
$W + X + Y + Z = 360°$
$Z = 360° − (W + X + Y)$
$280° + Z = 360° $ so $Z = 80°.$
Question 14 |
For all positive integers x, if 32x + 1 < $\dfrac{1}{2}$, what is a possible value for $\dfrac{9^{x + 4}}{27}$?
1474 | |
1648 | |
1896 | |
2187 |
Question 14 Explanation:
The correct answer is (D).
Simplify the given expression by rewriting 9 and 27 as exponents of base 3:
First, recall that:
$\dfrac{x^a}{x^b}$ = $x$$(a-b)$
We can rewrite the problem as:
$\dfrac{9^{x+4}}{27}$ $ = \dfrac{3^{2(x+4)}}{3^3}$ $ = 3^{2x+8-3}$ $ = 3^{2x+5}$
The question now becomes - what is a possible value for $3$$2x+5$$ ?$
Since $3$$2x+1$ < $\dfrac{1}{2}$ and $x$ is defined for all positive integers, the smallest value for $x$ is 1.
If $x = 1$, then $3$$2x+5$$ = 3$$7$$ = 2187.$ The other possible values are too small.
Simplify the given expression by rewriting 9 and 27 as exponents of base 3:
First, recall that:
$\dfrac{x^a}{x^b}$ = $x$$(a-b)$
We can rewrite the problem as:
$\dfrac{9^{x+4}}{27}$ $ = \dfrac{3^{2(x+4)}}{3^3}$ $ = 3^{2x+8-3}$ $ = 3^{2x+5}$
The question now becomes - what is a possible value for $3$$2x+5$$ ?$
Since $3$$2x+1$ < $\dfrac{1}{2}$ and $x$ is defined for all positive integers, the smallest value for $x$ is 1.
If $x = 1$, then $3$$2x+5$$ = 3$$7$$ = 2187.$ The other possible values are too small.
Question 15 |
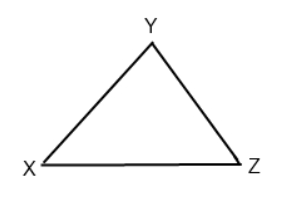 Point A lies between X and Y. Point B lies on YZ and Point C lies on XZ. BZ is congruent to CZ, and ∠XYZ = 90°. XZ – CZ = XA. What is the value of ∠ACB?
Point A lies between X and Y. Point B lies on YZ and Point C lies on XZ. BZ is congruent to CZ, and ∠XYZ = 90°. XZ – CZ = XA. What is the value of ∠ACB?
45° | |
60° | |
75° | |
90° |
Question 15 Explanation:
The correct answer is (A).
This is a Geometry question, so you’ll want to begin by drawing the figure on your own and filling in the given information. Let’s label∠ACB as z to keep track of it.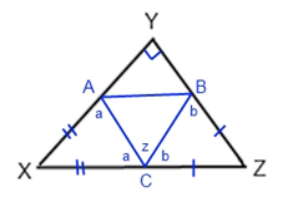
The problem tells us that XZ – CZ = XA. Looking at the triangle, we can also see that XZ – CZ = XC. Hence, sides XC and XA are equal, and so are the angles opposite them (denoted by a.)
Because a, z, and b are supplementary, $a + b + z = 180.$
We know that $∠X + ∠Y + ∠Z = 180°$. Simplifying, we get:
$∠X + 90° + ∠Z = 180°$
$∠X + ∠Z = 90°$
We also know that $∠X = 180 − 2a$ and $∠Z = 180 − 2b$
Substituting these values, we get: $(180 − 2b) + (180 − 2a) = 90$
Simplifying this second equation:
$360 − 2b − 2a = 90.$
Subtracting 360:
$−2b − 2a = −270 → 270 = 2a + 2b$
Let’s factor out the 2 from the variables:
$270 = 2(a + b)$
Now, let's go back to the very first equation. If we manipulate it, we can see that $a + b = 180 − z.$ Let’s substitute $180 − z$ for $a + b$:
$270 = 2(180 − z)$
$z = 45° = ∠ACB.$
This is a difficulty level 5 question.
This is a Geometry question, so you’ll want to begin by drawing the figure on your own and filling in the given information. Let’s label∠ACB as z to keep track of it.

The problem tells us that BZ and CZ are congruent. Thus, ∠ZBC and ∠ZCB (denoted by b for simplicity) are equal.
The problem tells us that XZ – CZ = XA. Looking at the triangle, we can also see that XZ – CZ = XC. Hence, sides XC and XA are equal, and so are the angles opposite them (denoted by a.)
Because a, z, and b are supplementary, $a + b + z = 180.$
We know that $∠X + ∠Y + ∠Z = 180°$. Simplifying, we get:
$∠X + 90° + ∠Z = 180°$
$∠X + ∠Z = 90°$
We also know that $∠X = 180 − 2a$ and $∠Z = 180 − 2b$
Substituting these values, we get: $(180 − 2b) + (180 − 2a) = 90$
Simplifying this second equation:
$360 − 2b − 2a = 90.$
Subtracting 360:
$−2b − 2a = −270 → 270 = 2a + 2b$
Let’s factor out the 2 from the variables:
$270 = 2(a + b)$
Now, let's go back to the very first equation. If we manipulate it, we can see that $a + b = 180 − z.$ Let’s substitute $180 − z$ for $a + b$:
$270 = 2(180 − z)$
$z = 45° = ∠ACB.$
This is a difficulty level 5 question.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 15 questions to complete.
|
List |
